题目内容
19.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\frac{{2\sqrt{2}}}{3}$|$\overrightarrow{b}$|,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥(3$\overrightarrow{a}$+2$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |
分析 根据向量垂直的等价条件以及向量数量积的应用进行求解即可.
解答 解:∵($\overrightarrow{a}$-$\overrightarrow{b}$)⊥(3$\overrightarrow{a}$+2$\overrightarrow{b}$),
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•(3$\overrightarrow{a}$+2$\overrightarrow{b}$)=0,
即3$\overrightarrow{a}$2-2$\overrightarrow{b}$2-$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即$\overrightarrow{a}$•$\overrightarrow{b}$=3$\overrightarrow{a}$2-2$\overrightarrow{b}$2=$\frac{2}{3}$$\overrightarrow{b}$2,
∴cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{\frac{2}{3}{\overrightarrow{b}}^{2}}{\frac{2\sqrt{2}}{3}{\overrightarrow{b}}^{2}}$=$\frac{\sqrt{2}}{2}$,
即<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{4}$,
故选:A
点评 本题主要考查向量夹角的求解,利用向量数量积的应用以及向量垂直的等价条件是解决本题的关键.


| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1+2$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
| A. | (0,$\frac{\sqrt{3}}{2}$] | B. | (0,$\frac{3}{4}$] | C. | [$\frac{\sqrt{3}}{2}$,1) | D. | [$\frac{3}{4}$,1) |
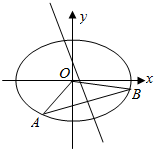 已知椭圆$\frac{x^2}{2}+{y^2}=1$上两个不同的点A,B关于直线y=mx+$\frac{1}{2}$对称.
已知椭圆$\frac{x^2}{2}+{y^2}=1$上两个不同的点A,B关于直线y=mx+$\frac{1}{2}$对称.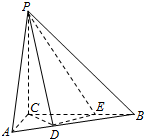 如题图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$.D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2EB=2.
如题图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$.D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2EB=2.