题目内容
10.设函数f(x)=e2x-alnx.(Ⅰ)讨论f(x)的导函数f′(x)零点的个数;
(Ⅱ)证明:当a>0时,f(x)≥2a+aln$\frac{2}{a}$.
分析 (Ⅰ)先求导,在分类讨论,当a≤0时,当a>0时,根据零点存在定理,即可求出;
(Ⅱ)设导函数f′(x)在(0,+∞)上的唯一零点为x0,根据函数f(x)的单调性得到函数的最小值f(x0),只要最小值大于2a+aln$\frac{2}{a}$,问题得以证明.
解答 解:(Ⅰ)f(x)=e2x-alnx的定义域为(0,+∞),
∴f′(x)=2e2x-$\frac{a}{x}$.
当a≤0时,f′(x)>0恒成立,故f′(x)没有零点,
当a>0时,∵y=e2x为单调递增,y=-$\frac{a}{x}$单调递增,
∴f′(x)在(0,+∞)单调递增,
又f′(a)>0,
假设存在b满足0<b<$\frac{a}{4}$时,且b<$\frac{1}{4}$,f′(b)<0,
故当a>0时,导函数f′(x)存在唯一的零点,
(Ⅱ)由(Ⅰ)知,可设导函数f′(x)在(0,+∞)上的唯一零点为x0,
当x∈(0,x0)时,f′(x)<0,
当x∈(x0+∞)时,f′(x)>0,
故f(x)在(0,x0)单调递减,在(x0+∞)单调递增,
所欲当x=x0时,f(x)取得最小值,最小值为f(x0),
由于$2{e}^{2{x}_{0}}$-$\frac{a}{{x}_{0}}$=0,
所以f(x0)=$\frac{a}{2{x}_{0}}$+2ax0+aln$\frac{2}{a}$≥2a+aln$\frac{2}{a}$.
故当a>0时,f(x)≥2a+aln$\frac{2}{a}$.
点评 本题考查了导数和函数单调性的关系和最值的关系,以及函数的零点存在定理,属于中档题.

练习册系列答案
相关题目
18.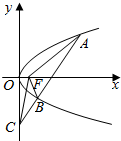 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( )
如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( )
 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( )
如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( )| A. | $\frac{{|{BF}|-1}}{{|{AF}|-1}}$ | B. | $\frac{{{{|{BF}|}^2}-1}}{{{{|{AF}|}^2}-1}}$ | C. | $\frac{{|{BF}|+1}}{{|{AF}|+1}}$ | D. | $\frac{{{{|{BF}|}^2}+1}}{{{{|{AF}|}^2}+1}}$ |
15.投篮测试中,每人投3次,至少投中2次才能通过测试.己知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )
| A. | 0.648 | B. | 0.432 | C. | 0.36 | D. | 0.312 |
19.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\frac{{2\sqrt{2}}}{3}$|$\overrightarrow{b}$|,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥(3$\overrightarrow{a}$+2$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |