题目内容
4．${（{{x^3}+\frac{1}{{2\sqrt{x}}}}）^5}$的展开式中x8的系数是$\frac{5}{2}$（用数字作答）．分析 先求出二项式展开式的通项公式，再令x的幂指数等于8，求得r的值，即可求得展开式中的x8的系数．
解答 解：由于${（{{x^3}+\frac{1}{{2\sqrt{x}}}}）^5}$的展开式的通项公式为 Tr+1=${C}_{5}^{r}$•$\frac{1}{{2}^{r}}$•${x}^{15-\frac{7r}{2}}$，
令15-$\frac{7r}{2}$=8，求得r=2，故开式中x8的系数是 ${C}_{5}^{2}$•$\frac{1}{4}$=$\frac{5}{2}$，
故答案为：$\frac{5}{2}$．
点评 本题主要考查二项式定理的应用，二项式展开式的通项公式，属于基础题．
练习册系列答案
快乐5加2金卷系列答案
相关题目
15．投篮测试中，每人投3次，至少投中2次才能通过测试．己知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为（ ）
| A． | 0.648 | B． | 0.432 | C． | 0.36 | D． | 0.312 |
19．若非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\frac{{2\sqrt{2}}}{3}$|$\overrightarrow{b}$|，且（$\overrightarrow{a}$-$\overrightarrow{b}$）⊥（3$\overrightarrow{a}$+2$\overrightarrow{b}$），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | $\frac{3π}{4}$ | D． | π |
16．“x=1”是“x2-2x+1=0”的（ ）
| A． | 充要条件 | B． | 充分而不必要条件 | ||
| C． | 必要而不充分条件 | D． | 既不充分也不必要条件 |
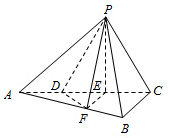如题图，三棱锥P-ABC中，平面PAC⊥平面ABC，∠ABC=$\frac{π}{2}$，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF∥BC．