题目内容
14.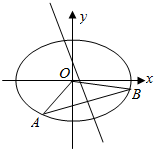 已知椭圆$\frac{x^2}{2}+{y^2}=1$上两个不同的点A,B关于直线y=mx+$\frac{1}{2}$对称.
已知椭圆$\frac{x^2}{2}+{y^2}=1$上两个不同的点A,B关于直线y=mx+$\frac{1}{2}$对称.(1)求实数m的取值范围;
(2)求△AOB面积的最大值(O为坐标原点).
分析 (1)由题意,可设直线AB的方程为x=-my+n,代入椭圆方程可得(m2+2)y2-2mny+n2-2=0,设A(x1,y1),B(x2,y2).可得△>0,设线段AB的中点P(x0,y0),利用中点坐标公式及其根与系数的可得P,代入直线y=mx+$\frac{1}{2}$,可得$n=-\frac{{m}^{2}+2}{2m}$,代入△>0,即可解出.
(2)直线AB与x轴交点横坐标为n,可得S△OAB=$\frac{1}{2}|n||{y}_{1}-{y}_{2}|$,再利用均值不等式即可得出.
解答 解:(1)由题意,可设直线AB的方程为x=-my+n,代入椭圆方程$\frac{{x}^{2}}{2}+{y}^{2}=1$,可得(m2+2)y2-2mny+n2-2=0,
设A(x1,y1),B(x2,y2).由题意,△=4m2n2-4(m2+2)(n2-2)=8(m2-n2+2)>0,
设线段AB的中点P(x0,y0),则${y}_{0}=\frac{{y}_{1}+{y}_{2}}{2}=\frac{mn}{{m}^{2}+2}$.x0=-m×$\frac{mn}{{m}^{2}+2}$+n=$\frac{2n}{{m}^{2}+2}$,
由于点P在直线y=mx+$\frac{1}{2}$上,∴$\frac{mn}{{m}^{2}+2}$=$\frac{2mn}{{m}^{2}+2}$+$\frac{1}{2}$,
∴$n=-\frac{{m}^{2}+2}{2m}$,代入△>0,可得3m4+4m2-4>0,
解得m2$>\frac{2}{3}$,∴$m<-\frac{\sqrt{6}}{3}$或m$>\frac{\sqrt{6}}{3}$.
(2)直线AB与x轴交点横坐标为n,
∴S△OAB=$\frac{1}{2}|n||{y}_{1}-{y}_{2}|$=$\frac{1}{2}$|n|•$•\frac{\sqrt{8({m}^{2}-{n}^{2}+2)}}{{m}^{2}+2}$=$\sqrt{2}\sqrt{\frac{{n}^{2}({m}^{2}-{n}^{2}+2)}{({m}^{2}+2)^{2}}}$,
由均值不等式可得:n2(m2-n2+2)$≤(\frac{{n}^{2}+{m}^{2}-{n}^{2}+2}{2})^{2}$=$\frac{({m}^{2}+2)^{2}}{4}$,
∴S△AOB$≤\sqrt{2}×\sqrt{\frac{1}{4}}$=$\frac{\sqrt{2}}{2}$,当且仅当n2=m2-n2+2,即2n2=m2+2,又∵$n=-\frac{{m}^{2}+2}{2m}$,解得m=$±\sqrt{2}$,
当且仅当m=$±\sqrt{2}$时,S△AOB取得最大值为$\frac{\sqrt{2}}{2}$.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标公式、线段垂直平分线的性质、三角形面积计算公式、弦长公式、均值不等式的性质,考查了推理能力与计算能力,属于难题.

| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |
| A. | -3 | B. | 1 | C. | $\frac{4}{3}$ | D. | 3 |
| A. | $\frac{12}{5}$ | B. | -$\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
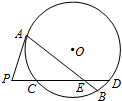 如题图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE:ED=2:1,则BE=2.
如题图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE:ED=2:1,则BE=2.