题目内容
8．在区间[0，5]上随机地选择一个数p，则方程x2+2px+3p-2=0有两个负根的概率为$\frac{2}{3}$．分析 由一元二次方程根的分布可得p的不等式组，解不等式组，由长度之比可得所求概率．
解答 解：方程x2+2px+3p-2=0有两个负根等价于$\left\{\begin{array}{l}{△=4{p}^{2}-4（3p-2）≥0}\\{{x}_{1}+{x}_{2}=-2p＜0}\\{{x}_{1}{x}_{2}=3p-2＞0}\end{array}\right.$，
解关于p的不等式组可得$\frac{2}{3}$＜p≤1或p≥2，
∴所求概率P=$\frac{1-\frac{2}{3}+5-2}{5-0}$=$\frac{2}{3}$
故答案为：$\frac{2}{3}$
点评 本题考查几何概型，涉及一元二次方程根的分布，属基础题．
练习册系列答案
名校课堂系列答案
相关题目
19．若非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\frac{{2\sqrt{2}}}{3}$|$\overrightarrow{b}$|，且（$\overrightarrow{a}$-$\overrightarrow{b}$）⊥（3$\overrightarrow{a}$+2$\overrightarrow{b}$），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | $\frac{3π}{4}$ | D． | π |
16．“x=1”是“x2-2x+1=0”的（ ）
| A． | 充要条件 | B． | 充分而不必要条件 | ||
| C． | 必要而不充分条件 | D． | 既不充分也不必要条件 |
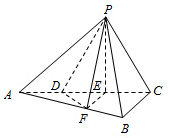如题图，三棱锥P-ABC中，平面PAC⊥平面ABC，∠ABC=$\frac{π}{2}$，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF∥BC．
如图，椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点A（0，-1），且离心率为$\frac{\sqrt{2}}{2}$．