题目内容
11. 如题图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$.D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2EB=2.
如题图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$.D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2EB=2.(Ⅰ)证明:DE⊥平面PCD
(Ⅱ)求二面角A-PD-C的余弦值.
分析 (Ⅰ)由已知条件易得PC⊥DE,CD⊥DE,由线面垂直的判定定理可得;
(Ⅱ)以C为原点,分别以$\overrightarrow{CA}$,$\overrightarrow{CB}$,$\overrightarrow{CP}$的方向为xyz轴的正方向建立空间直角坐标系,易得$\overrightarrow{ED}$,$\overrightarrow{DP}$,$\overrightarrow{DA}$的坐标,可求平面PAD的法向量$\overrightarrow{{n}_{1}}$,平面PCD的法向量$\overrightarrow{{n}_{2}}$可取$\overrightarrow{ED}$,由向量的夹角公式可得.
解答 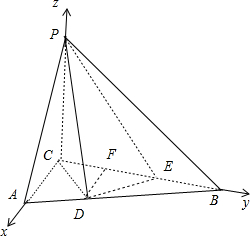 (Ⅰ)证明:∵PC⊥平面ABC,DE?平面ABC,∴PC⊥DE,
(Ⅰ)证明:∵PC⊥平面ABC,DE?平面ABC,∴PC⊥DE,
∵CE=2,CD=DE=$\sqrt{2}$,∴△CDE为等腰直角三角形,
∴CD⊥DE,∵PC∩CD=C,
DE垂直于平面PCD内的两条相交直线,
∴DE⊥平面PCD
(Ⅱ)由(Ⅰ)知△CDE为等腰直角三角形,∠DCE=$\frac{π}{4}$,
过点D作DF垂直CE于F,易知DF=FC=FE=1,又由已知EB=1,故FB=2,
由∠ACB=$\frac{π}{2}$得DF∥AC,$\frac{DF}{AC}=\frac{FB}{BC}=\frac{2}{3}$,故AC=$\frac{3}{2}$DF=$\frac{3}{2}$,
以C为原点,分别以$\overrightarrow{CA}$,$\overrightarrow{CB}$,$\overrightarrow{CP}$的方向为xyz轴的正方向建立空间直角坐标系,
则C(0,0,0),P(0,0,3),A($\frac{3}{2}$,0,0),E(0,2,0),D(1,1,0),
∴$\overrightarrow{ED}$=(1,-1,0),$\overrightarrow{DP}$=(-1,-1,3),$\overrightarrow{DA}$=($\frac{1}{2}$,-1,0),
设平面PAD的法向量$\overrightarrow{{n}_{1}}$=(x,y,z),由$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{DP}=-x-y+3z=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{DA}=\frac{1}{2}x-y=0}\end{array}\right.$,
故可取$\overrightarrow{{n}_{1}}$=(2,1,1),
由(Ⅰ)知DE⊥平面PCD,故平面PCD的法向量$\overrightarrow{{n}_{2}}$可取$\overrightarrow{ED}$=(1,-1,0),
∴两法向量夹角的余弦值cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{\sqrt{3}}{6}$
∴二面角A-PD-C的余弦值为$\frac{\sqrt{3}}{6}$.
点评 本题考查二面角,涉及直线与平面垂直的判定,建系化归为平面法向量的夹角是解决问题的关键,属难题.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
| A. | -3 | B. | 1 | C. | $\frac{4}{3}$ | D. | 3 |
| A. | y=$\sqrt{x}$ | B. | y=|sinx| | C. | y=cosx | D. | y=ex-e-x |
 如题图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE:ED=2:1,则BE=2.
如题图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE:ED=2:1,则BE=2.