题目内容
9.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x-4y=0交椭圆E于A,B两点,若|AF|+|BF|=4,点M到直线l的距离不小于$\frac{4}{5}$,则椭圆E的离心率的取值范围是( )| A. | (0,$\frac{\sqrt{3}}{2}$] | B. | (0,$\frac{3}{4}$] | C. | [$\frac{\sqrt{3}}{2}$,1) | D. | [$\frac{3}{4}$,1) |
分析 如图所示,设F′为椭圆的左焦点,连接AF′,BF′,则四边形AFBF′是平行四边形,可得4=|AF|+|BF|=|AF′|+|BF|=2a.取M(0,b),由点M到直线l的距离不小于$\frac{4}{5}$,可得$\frac{|4b|}{\sqrt{{3}^{2}+{4}^{2}}}$$≥\frac{4}{5}$,解得b≥1.再利用离心率计算公式e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$即可得出.
解答 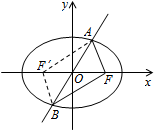 解:如图所示,设F′为椭圆的左焦点,连接AF′,BF′,则四边形AFBF′是平行四边形,
解:如图所示,设F′为椭圆的左焦点,连接AF′,BF′,则四边形AFBF′是平行四边形,
∴4=|AF|+|BF|=|AF′|+|AF|=2a,∴a=2.
取M(0,b),∵点M到直线l的距离不小于$\frac{4}{5}$,∴$\frac{|4b|}{\sqrt{{3}^{2}+{4}^{2}}}$$≥\frac{4}{5}$,解得b≥1.
∴e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$≤$\sqrt{1-\frac{1}{{2}^{2}}}$=$\frac{\sqrt{3}}{2}$.
∴椭圆E的离心率的取值范围是$(0,\frac{\sqrt{3}}{2}]$.
故选:A.
点评 本题考查了椭圆的定义标准方程及其性质、点到直线的距离公式、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
19.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\frac{{2\sqrt{2}}}{3}$|$\overrightarrow{b}$|,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥(3$\overrightarrow{a}$+2$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |
4.若sinα=-$\frac{5}{13}$,则α为第四象限角,则tanα的值等于( )
| A. | $\frac{12}{5}$ | B. | -$\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
1.下列函数为奇函数的是( )
| A. | y=$\sqrt{x}$ | B. | y=|sinx| | C. | y=cosx | D. | y=ex-e-x |
 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{\sqrt{2}}{2}$.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{\sqrt{2}}{2}$.