题目内容
7.设函数f(x)=(x-a)(x-b)(x-c)的导函数为f′(x),其中a,b.c是互不相等的常数,则f′(a)+f′(b)+f′(c)的值( )| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 以上都有可能 |
分析 分别求出f′(a),f′(b),f′(c)求和.
解答 解:f′(x)=(x-a)(x-b)+(x-b)(x-c)+(x-a)(x-c),
∴f′(a)=(a-b)(a-c)=a2-ab-ac+bc,
f′(b)=(b-a)(b-c)=b2-ab-bc+ac,
f′(c)=(c-a)(c-b)=c2-ac-bc+ab.
∴f′(a)+f′(b)+f′(c)=a2+b2+c2-ab-bc-ac.
∵a,b.c是互不相等的常数,
∴2(f′(a)+f′(b)+f′(c))=2a2+2b2+2c2-2ab-2bc-2ac
=(a-b)2+(b-c)2+(a-c)2>0.
故选:A.
点评 本题考查了导数运算,是基础题.

练习册系列答案
相关题目
2.函数y=Asin(ωx+φ)(ω>0)在一个周期内的图象如图所示,则ω的值是( )
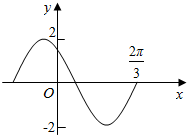

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.某校的教育教学水平不断提高,该校记录了2006年到2015年十年间每年考入清华大学、北京大学的人数和.为方便计算,2006年编号为1,2007年编号为2,…,2015年编号为10.数据如下:
(Ⅰ)从这10年中的后6年随机抽取两年,求考入清华大学、北京大学的人数和至少有一年多于20人的概率;
(Ⅱ)根据前5年的数据,利用最小二乘法求出y关于x的回归方程y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并计算2013年的估计值和实际值之间的差的绝对值.
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 年份(x) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 | 14 | 17 | 22 | 30 | 31 |
(Ⅱ)根据前5年的数据,利用最小二乘法求出y关于x的回归方程y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并计算2013年的估计值和实际值之间的差的绝对值.
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
3.函数f(x)=lg(x-1)+$\sqrt{4-{x}^{2}}$的定义域是( )
| A. | [1,2] | B. | (1,2] | C. | (1,+∞) | D. | [-2,2] |