题目内容
15.已知数列{an},{bn}的前n项和分别为Sn,Tn,其中an=2n-1,bn=$\frac{1}{{S}_{n}}$,设计算法求T100的值,并画出程序框图及编写程序.分析 由题意可得T100=$\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}+…+\frac{1}{10{0}^{2}}$,这是一个累加求和问题,共100项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.
解答  解:∵数列{an},{bn}的前n项和分别为Sn,Tn,其中an=2n-1,
解:∵数列{an},{bn}的前n项和分别为Sn,Tn,其中an=2n-1,
∴Sn=n2,bn=$\frac{1}{{n}^{2}}$,
∴T100=$\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}+…+\frac{1}{10{0}^{2}}$,
程序如下:
T=0
k=1
WHILE k≤100
T=T+$\frac{1}{{k}^{2}}$
k=k+1
WEND
PRINT T
END
框图如右图所示:
点评 本题主要考查设计程序框图解决实际问题.在一些算法中,也经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构.循环结构要在某个条件下终止循环,这就需要条件分支结构来判断.在循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用于输出结果,计数变量和累加变量一般是同步执行的,累加一次,计数一次.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
5.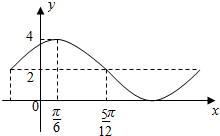 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )| A. | B=1 | B. | φ=$\frac{π}{6}$ | C. | ω=1 | D. | A=4 |
10.已知a>1,若函数f(x)=logax-ax有零点,则a的取值范围是( )
| A. | (1,e] | B. | (1,$\sqrt{e}$] | C. | (1,${e}^{\frac{1}{e}}$] | D. | (1,${e}^{\sqrt{e}-1}$] |
7.设函数f(x)=(x-a)(x-b)(x-c)的导函数为f′(x),其中a,b.c是互不相等的常数,则f′(a)+f′(b)+f′(c)的值( )
| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 以上都有可能 |