题目内容
2.函数y=Asin(ωx+φ)(ω>0)在一个周期内的图象如图所示,则ω的值是( )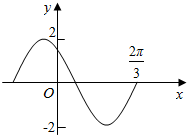
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设函数的周期为T,由函数图象可知:$\frac{T}{2}$<$\frac{2π}{3}$<$\frac{3T}{4}$,又T=$\frac{2π}{ω}$,ω>0,解得范围$\frac{3}{2}<ω<$$\frac{9}{4}$,结合选项可得ω的值.
解答 解:设函数的周期为T,由函数图象可知:$\frac{T}{2}$<$\frac{2π}{3}$<$\frac{3T}{4}$,
又T=$\frac{2π}{ω}$,ω>0,
∴$\frac{π}{ω}$<$\frac{2π}{3}$<$\frac{3π}{2ω}$,解得:$\frac{3}{2}<ω<$$\frac{9}{4}$,
结合选项可得:ω=2.
故选:B.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了周期公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知a>1,若函数f(x)=logax-ax有零点,则a的取值范围是( )
| A. | (1,e] | B. | (1,$\sqrt{e}$] | C. | (1,${e}^{\frac{1}{e}}$] | D. | (1,${e}^{\sqrt{e}-1}$] |
17.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x≥0}\\{2x-{x}^{2},x<0}\end{array}\right.$,若f(3-m2)<f(2m),则实数m的取值范围是( )
| A. | (-∞,-1) | B. | (3,+∞) | C. | (-∞,-3)∪(1,+∞) | D. | (-∞,-1)∪(3,+∞) |
7.设函数f(x)=(x-a)(x-b)(x-c)的导函数为f′(x),其中a,b.c是互不相等的常数,则f′(a)+f′(b)+f′(c)的值( )
| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 以上都有可能 |