题目内容
2.设x>0,y>0,x+$\frac{1}{x}$+$\frac{y}{2}$+$\frac{8}{y}$=10.则2x+y的最大值为18.分析 变形利用基本不等式的性质和一元二次不等式的解法即可得出.
解答 解:设2x+y=t(t>0),
x+$\frac{1}{x}$+$\frac{y}{2}$+$\frac{8}{y}$=10即为$\frac{1}{x}$+$\frac{8}{y}$=10-$\frac{1}{2}$t,
即有t(10-$\frac{1}{2}$t)=(2x+y)($\frac{1}{x}$+$\frac{8}{y}$)=10+$\frac{y}{x}$+$\frac{16x}{y}$
≥10+2$\sqrt{\frac{y}{x}•\frac{16x}{y}}$=18,
当且仅当y=4x,即x=3,y=12取得等号.
由t(10-$\frac{1}{2}$t)≥18,解得2≤t≤18.
可得2x+y的最大值为18.
故答案为:18.
点评 本题考查了用基本不等式的性质和一元二次不等式的解法,注意式子变形的运用,属于中档题.

练习册系列答案
相关题目
12.对函数f(x)=$\sqrt{3}sinxcosx+{cos}^{2}x-\frac{1}{2}$的表述错误的是( )
| A. | 最小正周期为π | |
| B. | 函数y=sin2x向左平移$\frac{π}{12}$个单位可得到f(x) | |
| C. | f(x)在区间$(-\frac{π}{3},\frac{π}{6})$上递增 | |
| D. | 点$(\frac{π}{6},0)$是f(x)的一个对称中心 |
13.定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有(x2-x1)[f(x2)-f(x1)]<0.则( )
| A. | f(1)<f(-2)<f(3) | B. | f(3)<f(1)<f(-2) | C. | f(一2)<f(1)<f(3) | D. | f(3)<f(-2)<f(1) |
10.直角坐标系中,方程|x|•y=1表示的曲线是( )
| A. | 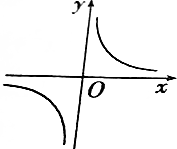 | B. | 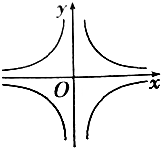 | ||
| C. | 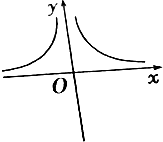 | D. | 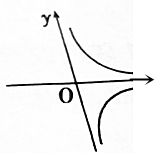 |
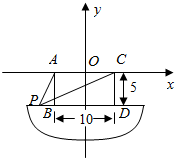 船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.
船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.