题目内容
设数列 {an} 中,a1=a,an+1+2an=2n+1(n∈N*).
(Ⅰ)若a1,a2,a3成等差数列,求实数a的值;
(Ⅱ)试问数列 {an} 能为等比数列吗?若能,试写出它的充要条件并加以证明;若不能,请说明理由.
(Ⅰ)若a1,a2,a3成等差数列,求实数a的值;
(Ⅱ)试问数列 {an} 能为等比数列吗?若能,试写出它的充要条件并加以证明;若不能,请说明理由.
解(Ⅰ)
 ,
,因为
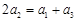 ,所以
,所以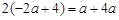 ,得
,得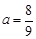 4分
4分(Ⅱ)方法一:因为
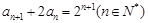 ,所以
,所以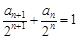 ,
,得:
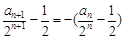 ,
,当
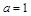 时,
时,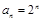 ,显然成立;
,显然成立;当
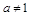 时,
时,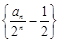 是以
是以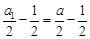 为首项,-1为公比的等比数列,
为首项,-1为公比的等比数列,所以
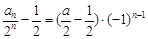 ,得:
,得: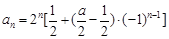
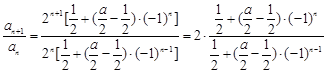
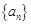 为等比数列
为等比数列 为常数,易得当且仅当
为常数,易得当且仅当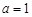 时,
时, 为常数。
为常数。方法二:因为
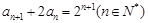 ,所以
,所以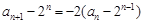 ,
,即
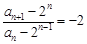 ,故
,故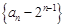 是以
是以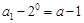 为首项,-2为公比的成等比数列,
为首项,-2为公比的成等比数列,所以
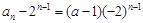 ,得:
,得: (下同解法一)
(下同解法一)方法三:由前三项成等比得
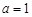 ,进而猜测
,进而猜测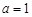 ,对于所有情况都成立,再证明。
,对于所有情况都成立,再证明。略

练习册系列答案
相关题目
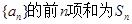 ,首项为1的等比数列
,首项为1的等比数列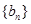 的公比为
的公比为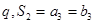 ,且
,且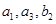 成等比数列。
成等比数列。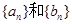 的通项公式;
的通项公式;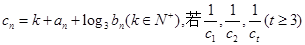 成等差数列,求k和t的值。
成等差数列,求k和t的值。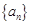 满足
满足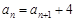 ,
,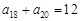 ,等比数列
,等比数列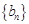 的首项为2,公比为
的首项为2,公比为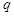 .
.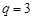 ,问
,问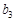 等于数列
等于数列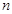 项和分别记为
项和分别记为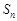 和
和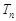 ,
,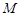 ,当
,当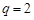 时,试比较
时,试比较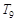 的大小
的大小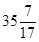 ,则插去的那个数为( ).
,则插去的那个数为( ).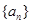 中,
中,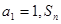 是数列
是数列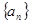 的前
的前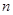 项和,对任意
项和,对任意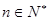 ,有
,有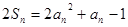 .函数
.函数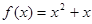 ,数列
,数列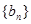 的首项
的首项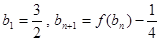
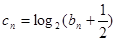 求证:
求证: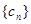 是等比数列并求
是等比数列并求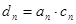 ,
, ,求数列
,求数列 的前n项和
的前n项和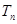 .
.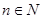 ,满足以下性质:(1)2&2=1,(2)(
,满足以下性质:(1)2&2=1,(2)(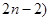 &2=(
&2=(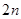 &2)+3,则2008&2的数值为
&2)+3,则2008&2的数值为 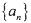 满足:
满足: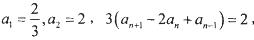
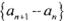 是等差数列;.
是等差数列;.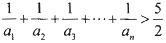 成立的最小的正整数n
成立的最小的正整数n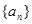 是等比数列,首项
是等比数列,首项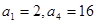 .
.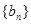 是等差数列,且
是等差数列,且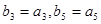 求数列
求数列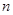 项和
项和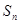 .
.  中,
中, 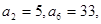 则
则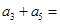 ______________
______________