题目内容
已知各项均为正数的数列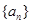 中,
中,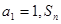 是数列
是数列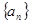 的前
的前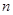 项和,对任意
项和,对任意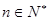 ,有
,有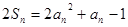 .函数
.函数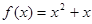 ,数列
,数列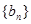 的首项
的首项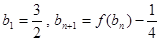
(Ⅰ)求数列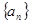 的通项公式;
的通项公式;
(Ⅱ)令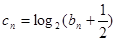 求证:
求证: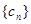 是等比数列并求
是等比数列并求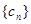 通项公式;
通项公式;
(Ⅲ)令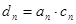 ,
, ,求数列
,求数列 的前n项和
的前n项和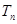 .
.
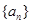 中,
中,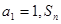 是数列
是数列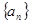 的前
的前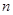 项和,对任意
项和,对任意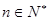 ,有
,有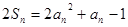 .函数
.函数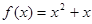 ,数列
,数列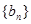 的首项
的首项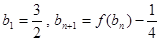
(Ⅰ)求数列
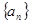 的通项公式;
的通项公式;(Ⅱ)令
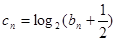 求证:
求证: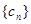 是等比数列并求
是等比数列并求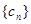 通项公式;
通项公式; (Ⅲ)令
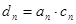 ,
, ,求数列
,求数列 的前n项和
的前n项和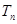 .
.(Ⅰ)由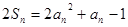 ①
①
得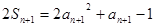 ② ---------1分
② ---------1分
由②—①,得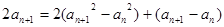
即: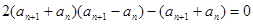 ---------2分
---------2分
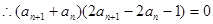 由于数列
由于数列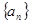 各项均为正数,
各项均为正数,
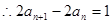 ------------3分
------------3分
即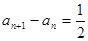
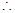 数列
数列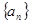 是首项为
是首项为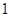 ,公差为
,公差为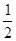 的等差数列,
的等差数列,
 数列
数列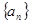 的通项公式是
的通项公式是 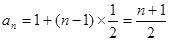 ----------4分
----------4分
(Ⅱ)由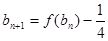 知
知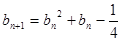 ,
,
所以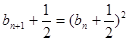 , ------------5分
, ------------5分
有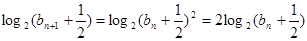 ,即
,即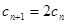 ,------6分
,------6分
而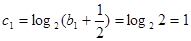 ,
,
故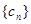 是以
是以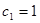 为首项,公比为2的等比数列。 所以
为首项,公比为2的等比数列。 所以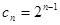 ----8分
----8分
(Ⅲ)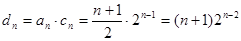 , -------9分
, -------9分
所以数列 的前n项和
的前n项和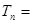
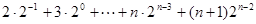
错位相减可得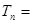
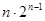
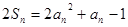 ①
①得
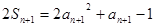 ② ---------1分
② ---------1分由②—①,得
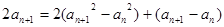
即:
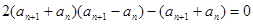 ---------2分
---------2分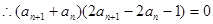 由于数列
由于数列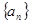 各项均为正数,
各项均为正数,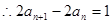 ------------3分
------------3分即
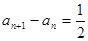
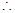 数列
数列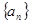 是首项为
是首项为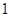 ,公差为
,公差为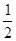 的等差数列,
的等差数列,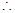 数列
数列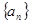 的通项公式是
的通项公式是 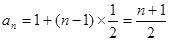 ----------4分
----------4分(Ⅱ)由
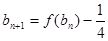 知
知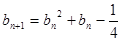 ,
,所以
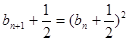 , ------------5分
, ------------5分有
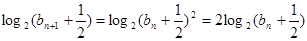 ,即
,即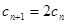 ,------6分
,------6分而
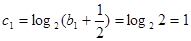 ,
,故
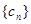 是以
是以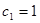 为首项,公比为2的等比数列。 所以
为首项,公比为2的等比数列。 所以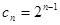 ----8分
----8分(Ⅲ)
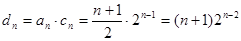 , -------9分
, -------9分所以数列
 的前n项和
的前n项和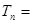
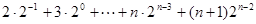
错位相减可得
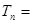
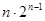
略

练习册系列答案
相关题目
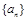 的前
的前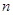 项和为
项和为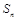 ,且满足
,且满足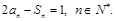
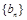 ,在
,在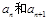 两项之间插入
两项之间插入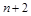 个数构成等差数列,求
个数构成等差数列,求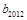 的值;
的值;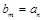 ,并求
,并求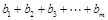 (用
(用
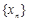 ,满足
,满足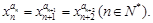
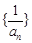 是等差数列;
是等差数列;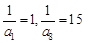 ,当
,当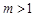 时, 不等式
时, 不等式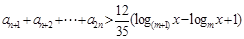 对
对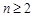 的正整数恒成立,求
的正整数恒成立,求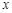 的取值范围.
的取值范围.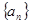 中,若
中,若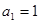 ,
,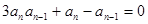
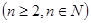 ,则通项
,则通项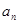 =( )
=( )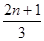
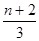
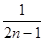
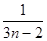
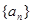 是等比数列,且
是等比数列,且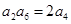 ,则
,则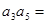 ( )
( )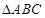 是边长为1的正三角形,曲线
是边长为1的正三角形,曲线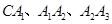 分别以
分别以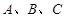 为圆心,
为圆心,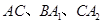 为半径画的弧,
为半径画的弧, 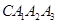 为曲线的第1圈,然后又以
为曲线的第1圈,然后又以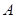 为圆心,
为圆心,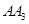 为半径画弧
为半径画弧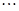 ,这样画到第
,这样画到第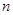 圈,则所得曲线
圈,则所得曲线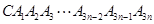 的总长度
的总长度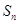 为( )
为( ) 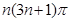
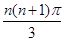
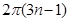
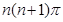
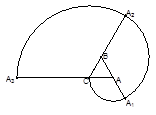
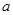 , b的等差中项是
, b的等差中项是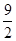 ,等比中项为2
,等比中项为2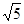 ,且
,且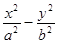 =1的离心率为 。
=1的离心率为 。