题目内容
【题目】已知函数
(1)求函数
解析式；
(2)判断函数的奇偶性（给出结论即可）；
(3)若方程
【答案】（1）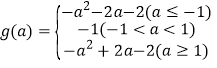
（2）偶函数（3）b<-1
【解析】
(1)将函数f(x)解析式进行化简，然后利用二次函数的图像的性质，讨论对称轴和区间的位置关系可得函数的最大值；（2）由函数图像可得函数的奇偶性；（3）根据题意可转为y=b与y=g(a)有两个不同的交点，结合图像可得b得取值范围.
(1)
=(sinxa)2-1，
∵1sinx1，∴当1<a<1时,函数的最大值为-1，
当a
1时，则当sinx=1时，函数有最大值为
，
当a
1时，当sinx=1时，函数有最大值
，所以函数f(x)的最大值
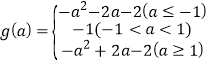
（2）函数g(x)为偶函数；
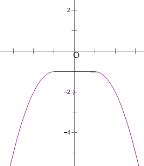
（3）若
画出函数g(a)的图像，由图像可得b<-1.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某种设备随着使用年限的增加，每年的维护费相应增加
现对一批该设备进行调查，得到这批设备自购入使用之日起，前五年平均每台设备每年的维护费用大致如表：
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 |
|
|
|
|
|
Ⅰ
求y关于t的线性回归方程；
Ⅱ若该设备的价格是每台5万元，甲认为应该使用满五年换一次设备，而乙则认为应该使用满十年换一次设备，你认为甲和乙谁更有道理？并说明理由．
参考公式：
，
