题目内容
【题目】设函数f(x)=x3﹣ax﹣b,x∈R,其中a,b∈R. (Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)存在极值点x0 , 且f(x1)=f(x0),其中x1≠x0;求证:x1+2x0=0.
【答案】解:(Ⅰ)若f(x)=x3﹣ax﹣b,则f′(x)=3x2﹣a, 分两种情况讨论:
①、当a≤0时,有f′(x)=3x2﹣a≥0恒成立,
此时f(x)的单调递增区间为(﹣∞,+∞),
②、当a>0时,令f′(x)=3x2﹣a=0,解得x=﹣ ![]() 或x=
或x= ![]() ,
,
当x> ![]() 或x<﹣
或x<﹣ ![]() 时,f′(x)=3x2﹣a>0,f(x)为增函数,
时,f′(x)=3x2﹣a>0,f(x)为增函数,
当﹣ ![]() <x<
<x< ![]() 时,f′(x)=3x2﹣a<0,f(x)为减函数,
时,f′(x)=3x2﹣a<0,f(x)为减函数,
故f(x)的增区间为(﹣∞,﹣ ![]() ),(
),( ![]() ,+∞),减区间为(﹣
,+∞),减区间为(﹣ ![]() ,
, ![]() );
);
(Ⅱ)若f(x)存在极值点x0 , 则必有a>0,且x0≠0,
由题意可得,f′(x)=3x2﹣a,则x02= ![]() ,
,
进而f(x0)=x03﹣ax0﹣b=﹣ ![]() x0﹣b,
x0﹣b,
又f(﹣2x0)=﹣8x03+2ax0﹣b=﹣ ![]() x0+2ax0﹣b=f(x0),
x0+2ax0﹣b=f(x0),
由题意及(Ⅰ)可得:存在唯一的实数x1 , 满足f(x1)=f(x0),其中x1≠x0 ,
则有x1=﹣2x0 , 故有x1+2x0=0
【解析】(Ⅰ)求出f(x)的导数,讨论a≤0时f′(x)≥0,f(x)在R上递增;当a>0时,由导数大于0,可得增区间;导数小于0,可得减区间;(Ⅱ)由条件判断出a>0,且x0≠0,由f′(x0)=0求出x0 , 分别代入解析式化简f(x0),f(﹣2x0),化简整理后可得证.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】现从某医院中随机抽取了7位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1)
附:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
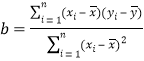 ,
,![]() .
.
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+![]() )(ω>0,|
)(ω>0,|![]() |
|![]() )在某一个周期内的图象时,列表并填入了部分数据,如下表:
)在某一个周期内的图象时,列表并填入了部分数据,如下表:
ωx+ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+ | 0 | 5 | ﹣5 | 0 |
(1)请在答题卡上将如表数据补充完整,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动![]() 个单位长度,得到y=g(x)图象,求y=g(x)的图象离原点O最近的对称中心.
个单位长度,得到y=g(x)图象,求y=g(x)的图象离原点O最近的对称中心.