题目内容
【题目】已知F1 , F2是椭圆C: ![]() +
+ ![]() =1的左、右焦点.
=1的左、右焦点.
(1)若点M在椭圆C上,且∠F1MF2=60°,求△F1MF2的面积;
(2)动直线y=k(x+1)与椭圆C相交于A,B两点,点T(t,0),问是否存在t∈R,使得 ![]()
![]() 为定值,若存在求出t的值,若不存在,请说明理由.
为定值,若存在求出t的值,若不存在,请说明理由.
【答案】
(1)解:∵a2=5,b2= ![]() ,c2=a2﹣b2=
,c2=a2﹣b2= ![]() ,
,
设丨PF1丨=m,丨PF2丨=n,
∵ 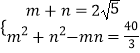 ,解得:mn=
,解得:mn= ![]() ,
,
∴△F1MF2的面积S,S= ![]() mnsin60°=
mnsin60°= ![]()
(2)解:设A(x1,y1),B(x2,y2),
∴ 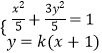 ,化简得:(3k2+1)x2+6k2x+3k2﹣5=0
,化简得:(3k2+1)x2+6k2x+3k2﹣5=0
由韦达定理可知:x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
由直线恒过椭圆内一点(﹣1,0),则定有两个交点,
∵ ![]() =(x1﹣t,y1),
=(x1﹣t,y1), ![]() =(x2﹣t,y2),
=(x2﹣t,y2),
∴ ![]()
![]() =(x1﹣t,y1)(x2﹣t,y2)=x1x2﹣t(x1+x2)+t2+y1y2,
=(x1﹣t,y1)(x2﹣t,y2)=x1x2﹣t(x1+x2)+t2+y1y2,
=x1x2﹣t(x1+x2)+t2+k2[x1x2+(x1+x2)+1],
= ![]() ,
,
令 ![]() =3,解得:t=﹣
=3,解得:t=﹣ ![]() ,
,
故存在,t=﹣ ![]()
【解析】(1)由题意可知,求得a,b和c的值,设丨PF1丨=m,丨PF2丨=n,根据椭圆的定义即可求得mn= ![]() ,由三角形的面积公式,即可求得S=
,由三角形的面积公式,即可求得S= ![]() mnsin60°=
mnsin60°= ![]() ;(2)将直线方程代入椭圆方程,由韦达定理求得x1+x2 , x1x2 ,
;(2)将直线方程代入椭圆方程,由韦达定理求得x1+x2 , x1x2 , ![]() =(x1﹣t,y1),
=(x1﹣t,y1), ![]() =(x2﹣t,y2),根据向量数量积的坐标表示,
=(x2﹣t,y2),根据向量数量积的坐标表示, ![]()
![]() =(x1﹣t,y1)(x2﹣t,y2)=x1x2﹣t(x1+x2)+t2+y1y2 ,
=(x1﹣t,y1)(x2﹣t,y2)=x1x2﹣t(x1+x2)+t2+y1y2 , ![]() =3,即可求得t=﹣
=3,即可求得t=﹣ ![]() ,故存在在t∈R,使得
,故存在在t∈R,使得 ![]()
![]() 为定值.
为定值.

练习册系列答案
相关题目
