题目内容
【题目】正方体ABCD﹣A1B1C1D1 ， E，F分别是上底面A1B1C1D1和侧面CDD1C1的中心，若 
=x 
+y 
+z 
，则x+y+z= ．
【答案】
【解析】解：如图，由题意可知：连接AC，BC交点为O，则点E在平面ABCD内的射影为O， ∴ 
= 
+ 
+ 
，①
点F在平面ABCD内的射影为M，
∴ 
= + + ，②
②﹣①× 得： ﹣ = 
+ 
，
∴ = + + ，
∴x+y+z= ，
所以答案是： ．
【考点精析】根据题目的已知条件，利用平面向量的基本定理及其意义的相关知识可以得到问题的答案，需要掌握如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
．
【题目】为调查乘客的候车情况，公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间（单位：分钟）作为样本分成5组，如下表所示：
组别 | 候车时间 | 人数 |
一 | [0，5） | 2 |
二 | [5，10） | 6 |
三 | [10，15） | 4 |
四 | [15，20） | 2 |
五 | [20，25] | 1 |
（Ⅰ）求这15名乘客的平均候车时间；
（Ⅱ）估计这60名乘客中候车时间少于10分钟的人数；
（Ⅲ）若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查，求抽到的两人恰好来自不同组的概率．
【题目】某同学用“五点法”画函数
在某一个周期内的图象时，列表并填入了部分数据，如下表：
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
（1）请将上表数据补充完整；函数
的解析式为
（直接写出结果即可）；
（2）根据表格中的数据作出
一个周期的图象；
（3）求函数在区间
上的最大值和最小值．
【题目】现从某医院中随机抽取了7位医护人员的关爱患者考核分数（患者考核：10分制），用相关的特征量
表示；医护专业知识考核分数（试卷考试：100分制），用相关的特征量
表示，数据如下表：
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
（1）求关于的线性回归方程（计算结果精确到0.01）；
（2）利用（1）中的线性回归方程，分析医护专业考核分数的变化对关爱患者考核分数的影响，并估计某医护人员的医护专业知识考核分数为95分时，他的关爱患者考核分数（精确到0.1）
附：回归直线方程
中斜率和截距的最小二乘法估计公式分别为
，
.
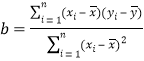