题目内容
(本小题满分16分)设函数f(x)=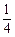 x4+bx2+cx+d,当x=t1时,f(x)有极小值.
x4+bx2+cx+d,当x=t1时,f(x)有极小值.
(1)若b=-6时,函数f(x)有极大值,求实数c的取值范围;
(2)在(1)的条件下,若存在实数c,使函数f(x)在闭区间[m-2,m+2]上单调递增,求实数m的取值范围;
(3)若函数f(x)只有一个极值点,且存在t2∈(t1,t1+1),使f ′(t2)=0,证明:函数g(x)=f(x)-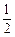 x2+t1x在区间(t1,t2)内最多有一个零点.
x2+t1x在区间(t1,t2)内最多有一个零点.
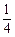 x4+bx2+cx+d,当x=t1时,f(x)有极小值.
x4+bx2+cx+d,当x=t1时,f(x)有极小值.(1)若b=-6时,函数f(x)有极大值,求实数c的取值范围;
(2)在(1)的条件下,若存在实数c,使函数f(x)在闭区间[m-2,m+2]上单调递增,求实数m的取值范围;
(3)若函数f(x)只有一个极值点,且存在t2∈(t1,t1+1),使f ′(t2)=0,证明:函数g(x)=f(x)-
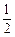 x2+t1x在区间(t1,t2)内最多有一个零点.
x2+t1x在区间(t1,t2)内最多有一个零点.(1)-16<c<16.(2)-2<m<0,或m>4.(3)同解析
(1)因为 f(x)=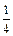 x4+bx2+cx+d,
x4+bx2+cx+d,
所以h(x)=f ′(x)=x3-12x+c.……2分
由题设,方程h(x)=0有三个互异的实根.
考察函数h(x)=x3-12x+c,则h ′(x)=0,得x=±2.
所以 故-16<c<16. ………………………………………………5分
故-16<c<16. ………………………………………………5分
(2)存在c∈(-16,16),使f ′(x)≥0,即x3-12x≥-c, (*)
所以x3-12x>-16,
即(x-2)2(x+4)>0(*)在区间[m-2,m+2]上恒成立. …………7分
所以[m-2,m+2]是不等式(*)解集的子集.
所以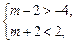 或m-2>2,即-2<m<0,或m>4. ………………………9分
或m-2>2,即-2<m<0,或m>4. ………………………9分
(3)由题设,可得存在α,β∈R,
使f ′(x)=x3+2bx+c=(x-t1)(x2+αx+β),
且x2+αx+β≥0恒成立.又f´(t2)=0,且在x=t2两侧同号,
所以f´(x) =(x-t1)(x-t2)2.
另一方面,
g ′(x)=x3+(2b-1)x+t1+c=x3+2bx+c-(x-t1)=(x-t1)[(x-t2)2-1].
因为 t1 < x < t2,且 t2-t1<1,所以-1< t1-t2 < x-t2 <0.所以 0<(x-t2)2<1,
所以(x-t2)2-1<0.
而 x-t1>0,所以g ′(x)<0,所以g(x)在(t1,t2)内单调减.
从而g(x)在(t1,t2)内最多有一个零点.…………………………………16分
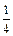 x4+bx2+cx+d,
x4+bx2+cx+d,所以h(x)=f ′(x)=x3-12x+c.……2分
由题设,方程h(x)=0有三个互异的实根.
考察函数h(x)=x3-12x+c,则h ′(x)=0,得x=±2.
| x | (-∞,-2) | -2 | (-2,2) | 2 | (2,+∞) |
| h ′(x) | + | 0 | - | 0 | + |
| h(x) | 增 | c+16 (极大值) | 减 | c-16( 极小值) | 增 |
 故-16<c<16. ………………………………………………5分
故-16<c<16. ………………………………………………5分(2)存在c∈(-16,16),使f ′(x)≥0,即x3-12x≥-c, (*)
所以x3-12x>-16,
即(x-2)2(x+4)>0(*)在区间[m-2,m+2]上恒成立. …………7分
所以[m-2,m+2]是不等式(*)解集的子集.
所以
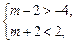 或m-2>2,即-2<m<0,或m>4. ………………………9分
或m-2>2,即-2<m<0,或m>4. ………………………9分(3)由题设,可得存在α,β∈R,
使f ′(x)=x3+2bx+c=(x-t1)(x2+αx+β),
且x2+αx+β≥0恒成立.又f´(t2)=0,且在x=t2两侧同号,
所以f´(x) =(x-t1)(x-t2)2.
另一方面,
g ′(x)=x3+(2b-1)x+t1+c=x3+2bx+c-(x-t1)=(x-t1)[(x-t2)2-1].
因为 t1 < x < t2,且 t2-t1<1,所以-1< t1-t2 < x-t2 <0.所以 0<(x-t2)2<1,
所以(x-t2)2-1<0.
而 x-t1>0,所以g ′(x)<0,所以g(x)在(t1,t2)内单调减.
从而g(x)在(t1,t2)内最多有一个零点.…………………………………16分

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
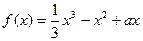 ,
,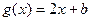 ,当
,当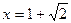 时,
时,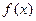 取得极值;
取得极值;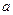 的值,并判断
的值,并判断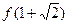 是函数
是函数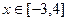 时,函数
时,函数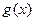 的图象有两个公共点,求
的图象有两个公共点,求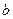 的取值范围;
的取值范围;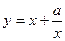 有如下性质:如果常数
有如下性质:如果常数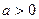 ,那么该函数在
,那么该函数在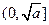 上是减函数,
上是减函数,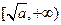 上是增函数,
上是增函数,
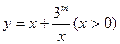 的值域是
的值域是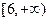 ,求实数
,求实数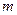 的值;
的值;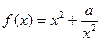 (常数
(常数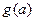 ,
,
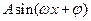 (其中A>0,
(其中A>0,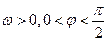 )的图象如图所示。
)的图象如图所示。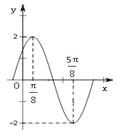
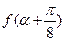 的值。
的值。 是偶函数,
是偶函数, 是奇函数,
是奇函数, 它们的定义域均为[-3,3],且它们在
它们的定义域均为[-3,3],且它们在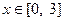 上的图像如图所示,则不等式
上的图像如图所示,则不等式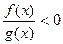 的解集是 _____.
的解集是 _____.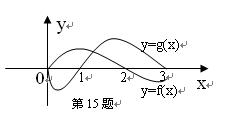
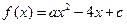 的值域为
的值域为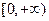 ,则
,则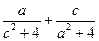 的最小值为 .
的最小值为 . D
D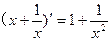
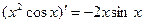
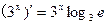
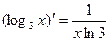 学
学 ,
,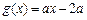 .若存在
.若存在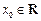 ,使得
,使得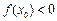 与
与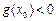 同时成立,则实数a的取值范围是 .
同时成立,则实数a的取值范围是 .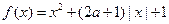 (
(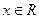 )有两个极小值点,则实数
)有两个极小值点,则实数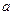 的取值范围是 .
的取值范围是 .