题目内容
(本小题满分14分)
已知函数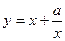 有如下性质:如果常数
有如下性质:如果常数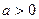 ,那么该函数在
,那么该函数在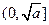 上是减函数,
上是减函数,
在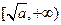 上是增函数,
上是增函数,

(Ⅰ)如果函数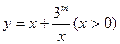 的值域是
的值域是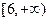 ,求实数
,求实数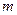 的值;
的值;
(Ⅱ)研究函数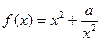 (常数
(常数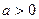 )在定义域内的单调性,并说明理由;
)在定义域内的单调性,并说明理由;
(Ⅲ)若把函数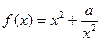 (常数
(常数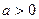 )在[1,2]上的最小值记为
)在[1,2]上的最小值记为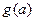 ,
,
求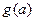 的表达式
的表达式
已知函数
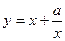 有如下性质:如果常数
有如下性质:如果常数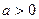 ,那么该函数在
,那么该函数在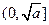 上是减函数,
上是减函数,在
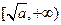 上是增函数,
上是增函数,

(Ⅰ)如果函数
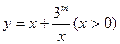 的值域是
的值域是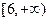 ,求实数
,求实数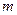 的值;
的值;(Ⅱ)研究函数
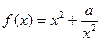 (常数
(常数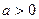 )在定义域内的单调性,并说明理由;
)在定义域内的单调性,并说明理由;(Ⅲ)若把函数
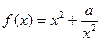 (常数
(常数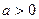 )在[1,2]上的最小值记为
)在[1,2]上的最小值记为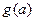 ,
,求
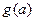 的表达式
的表达式
m=2,∴当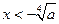 或
或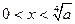 时,
时,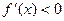 ,得
,得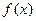 在
在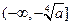 、
、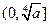 上是减函数,
上是减函数,
当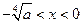 或
或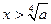 时,
时,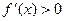 ,得
,得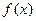 在
在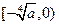 、
、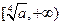 上是增函数
上是增函数
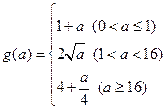
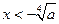 或
或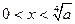 时,
时,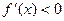 ,得
,得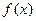 在
在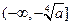 、
、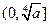 上是减函数,
上是减函数,当
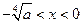 或
或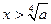 时,
时,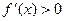 ,得
,得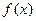 在
在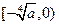 、
、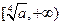 上是增函数
上是增函数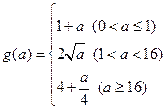
 (Ⅱ) 由题设知:
(Ⅱ) 由题设知: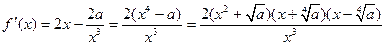 (6分)
(6分)∴当
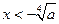 或
或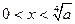 时,
时,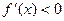 ,得
,得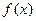 在
在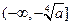 、
、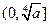 上是减函数,
上是减函数,当
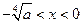 或
或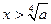 时,
时,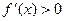 ,得
,得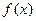 在
在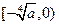 、
、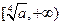 上是增函数。
上是增函数。(10分)
(Ⅲ)由(Ⅱ)知,
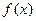 在
在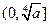 上是减函数,在
上是减函数,在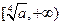 上是增函数,
上是增函数,∴当
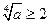 ,即
,即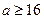 时,
时,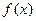 在
在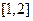 上是减函数,得
上是减函数,得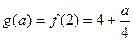 (11分)
(11分)当
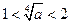 ,即
,即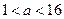 时,
时,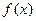 在
在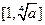 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,得
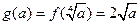 , (12分)
, (12分)当
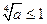 ,即
,即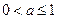 时,
时,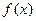 在
在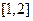 上是增函数,得
上是增函数,得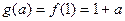 .(13分)
.(13分) ∴
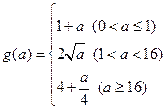 . (14分)
. (14分)
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
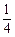 x4+bx2+cx+d,当x=t1时,f(x)有极小值.
x4+bx2+cx+d,当x=t1时,f(x)有极小值.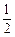 x2+t1x在区间(t1,t2)内最多有一个零点.
x2+t1x在区间(t1,t2)内最多有一个零点.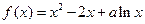 。
。 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数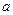 的取值范围;
的取值范围;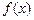 满足
满足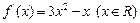 ,试写出一个符合题意的函数
,试写出一个符合题意的函数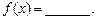
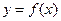 的图象与
的图象与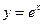 的图象关于直线
的图象关于直线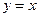 对称,则函数
对称,则函数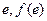 )处的切线方程为 .
)处的切线方程为 .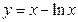 的单调递减区间是
的单调递减区间是 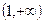
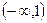
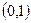
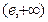
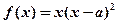 在
在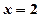 处有极大值,则
处有极大值,则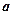 = 。
= 。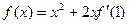 ,则
,则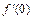 等于( )
等于( )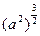 =a3 ,②
=a3 ,②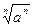 =|a| ,③函数y=
=|a| ,③函数y=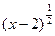 -(3x-7)0的定义域是(2, +∞), ④若
-(3x-7)0的定义域是(2, +∞), ④若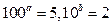 ,则2a+b=1其中正确的个数是
,则2a+b=1其中正确的个数是