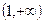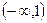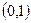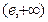题目内容
设函数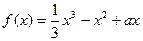 ,
,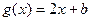 ,当
,当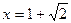 时,
时,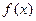 取得极值;
取得极值;
(1) 求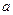 的值,并判断
的值,并判断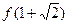 是函数
是函数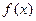 的极大值还是极小值;
的极大值还是极小值;
(2) 当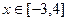 时,函数
时,函数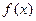 与
与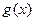 的图象有两个公共点,求
的图象有两个公共点,求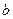 的取值范围;
的取值范围;
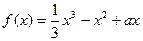 ,
,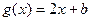 ,当
,当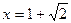 时,
时,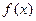 取得极值;
取得极值;(1) 求
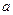 的值,并判断
的值,并判断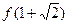 是函数
是函数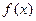 的极大值还是极小值;
的极大值还是极小值;(2) 当
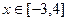 时,函数
时,函数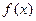 与
与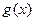 的图象有两个公共点,求
的图象有两个公共点,求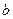 的取值范围;
的取值范围;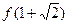 是函数
是函数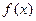 的极小值;,
的极小值;,
解:(1)由题意 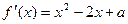
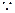 当
当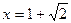 时,
时,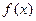 取得极值,
取得极值,
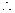
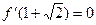

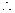 即
即 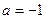
此时当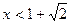 时,
时,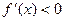 ,当
,当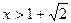 时,
时,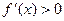 ,
,
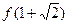 是函数
是函数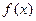 的极小值; ---------------------4分
的极小值; ---------------------4分
 (2)设
(2)设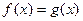 ,则
,则 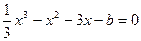 ,
,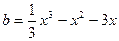
设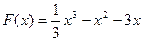 ,
,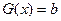
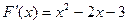 ,令
,令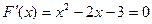 解得
解得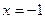 或
或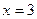 , 列表如下:
, 列表如下:
 函数
函数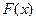 在
在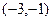 和
和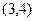 上是增函数,在
上是增函数,在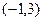 上是减函数;
上是减函数;
当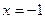 时,
时,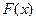 有极大值
有极大值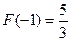 ;当
;当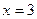 时,
时,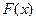 有极小值
有极小值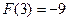 ;
;
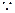 函数
函数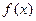 与
与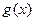 的图象有两个公共点,
的图象有两个公共点,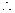 函数
函数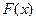 与
与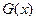 的图象有两个公共点
的图象有两个公共点
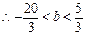 或
或 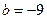
 ---------------------14分..
---------------------14分..
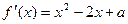
 当
当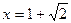 时,
时,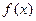 取得极值,
取得极值,
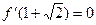

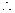 即
即 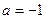
此时当
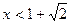 时,
时,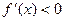 ,当
,当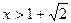 时,
时,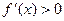 ,
,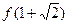 是函数
是函数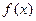 的极小值; ---------------------4分
的极小值; ---------------------4分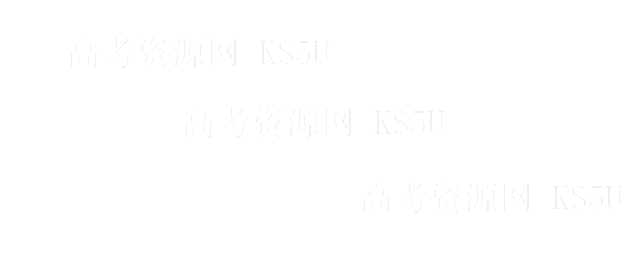 (2)设
(2)设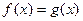 ,则
,则 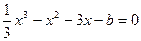 ,
,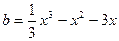
设
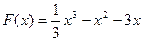 ,
,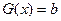
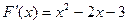 ,令
,令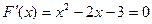 解得
解得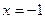 或
或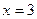 , 列表如下:
, 列表如下: 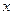 | 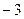 | 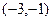 | 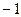 | 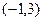 | 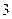 | 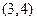 | 4 |
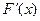 | | 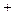 | 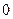 | __ | 0 | + | |
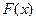 | 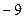 |   | 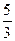 |   | 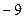 |  | 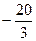 |
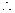 函数
函数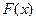 在
在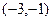 和
和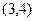 上是增函数,在
上是增函数,在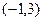 上是减函数;
上是减函数;当
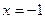 时,
时,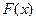 有极大值
有极大值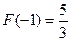 ;当
;当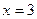 时,
时,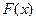 有极小值
有极小值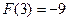 ;
; 函数
函数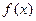 与
与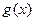 的图象有两个公共点,
的图象有两个公共点, 函数
函数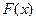 与
与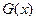 的图象有两个公共点
的图象有两个公共点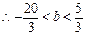 或
或 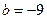
 ---------------------14分..
---------------------14分..
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
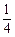 x4+bx2+cx+d,当x=t1时,f(x)有极小值.
x4+bx2+cx+d,当x=t1时,f(x)有极小值.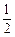 x2+t1x在区间(t1,t2)内最多有一个零点.
x2+t1x在区间(t1,t2)内最多有一个零点.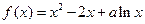 。
。 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数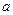 的取值范围;
的取值范围;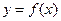 的图象与
的图象与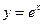 的图象关于直线
的图象关于直线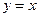 对称,则函数
对称,则函数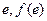 )处的切线方程为 .
)处的切线方程为 .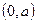 的直线与曲线
的直线与曲线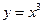 和
和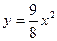 都相切,则
都相切,则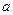 的值为
的值为 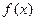 是以
是以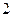 为周期的偶函数,且当
为周期的偶函数,且当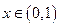 时,
时,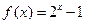 ,则
,则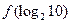 的值为( )
的值为( ) 
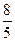
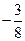
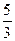
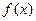 的反函数
的反函数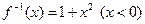 ,则
,则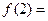
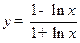 的导数为 ( )
的导数为 ( )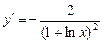
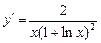
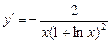
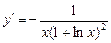
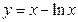 的单调递减区间是
的单调递减区间是