题目内容
6.已知数列{an}和{bn}满足a1=2,b1=1,an+1=2an(n∈N*),b1+$\frac{1}{2}$b2+$\frac{1}{3}$b3+…+$\frac{1}{n}$bn=bn+1-1(n∈N*)(Ⅰ)求an与bn;
(Ⅱ)记数列{anbn}的前n项和为Tn,求Tn.
分析 (Ⅰ)直接由a1=2,an+1=2an,可得数列{an}为等比数列,由等比数列的通项公式求得数列{an}的通项公式;
再由b1=1,b1+$\frac{1}{2}$b2+$\frac{1}{3}$b3+…+$\frac{1}{n}$bn=bn+1-1,取n=1求得b2=2,当n≥2时,得另一递推式,作差得到$\frac{1}{n}{b}_{n}={b}_{n+1}-{b}_{n}$,整理得数列{$\frac{{b}_{n}}{n}$}为常数列,由此可得{bn}的通项公式;
(Ⅱ)求出${a}_{n}{b}_{n}=n•{2}^{n}$,然后利用错位相减法求数列{anbn}的前n项和为Tn.
解答 解:(Ⅰ)由a1=2,an+1=2an,得${a}_{n}={2}^{n}(n∈{N}^{*})$.
由题意知,当n=1时,b1=b2-1,故b2=2,
当n≥2时,b1+$\frac{1}{2}$b2+$\frac{1}{3}$b3+…+$\frac{1}{n-1}{b}_{n-1}$=bn-1,和原递推式作差得,
$\frac{1}{n}{b}_{n}={b}_{n+1}-{b}_{n}$,整理得:$\frac{{b}_{n+1}}{n+1}=\frac{{b}_{n}}{n}$,
∴${b}_{n}=n(n∈{N}^{*})$;
(Ⅱ)由(Ⅰ)知,${a}_{n}{b}_{n}=n•{2}^{n}$,
因此${T}_{n}=2+2•{2}^{2}+3•{2}^{3}+…+n•{2}^{n}$
$2{T}_{n}={2}^{2}+2•{2}^{3}+3•{2}^{4}+…+n•{2}^{n+1}$,
两式作差得:$-{T}_{n}=2+{2}^{2}+…+{2}^{n}-n•{2}^{n+1}=\frac{2(1-{2}^{n})}{1-2}-n•{2}^{n+1}$,
${T}_{n}=(n-1)•{2}^{n+1}+2$(n∈N*).
点评 本题主要考查等差数列的通项公式、等差数列和等比数列等基础知识,同时考查数列求和等基本思想方法,以及推理论证能力,是中档题.

| A. | 7 | B. | 8 | C. | 9 | D. | 14 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | 1:6 | B. | 1:5 | C. | 1:4 | D. | 1:3 |
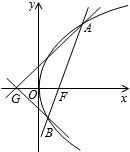 已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3,
已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3,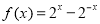 ,数列
,数列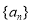 满足
满足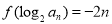 .
.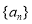 的通项公式;
的通项公式;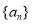 是递减数列.
是递减数列.