题目内容
6.已知函数f(x)=x2+ax(x≠0,a∈R).(1)判断函数f(x)的奇偶性;
(2)当a=1时,若存在x1∈[1,+∞)和任意的x2∈[1,+∞)使得f(x1)<log2(x2+m)成立,求实数m的取值范围.
分析 (1)分类讨论,根据函数的奇偶性的定义即可得到结论;
(2)设g(x)=log2(x+m),由题意f(x)min<g(x)min,分别根据函数的单调性求出两个函数的最小值,问题得以解决.
解答 解:(1)∵f(x)=x2+ax,
∴f(-x)=x2-ax,
当a=0时,f(-x)=x2=f(x)为偶函数,
当a≠0时,f(x)为非奇非偶函数,
(2)当a=1时,f(x)=x2+1x,x∈[1,+∞)
∴f′(x)=2x-1x2>0在[1,+∞)恒成立,
∴f(x)min=f(1)=1,
设g(x)=log2(x+m),
∵g(x)在[1,+∞)单调递增,
∴g(x)min=g(1)=log2(1+m),
∵存在x1∈[1,+∞)和任意的x2∈[1,+∞)使得f(x1)<log2(x2+m)成立,
∴f(x)min<g(x)min,
∴1<log2(1+m),
解得m>1,
故实数m的取值范围为(1,+∞)
点评 本题考查了函数奇偶性和参数的取值范围,关键根据函数的单调性求出函数最值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.设方程log2x-(12)x=0与log14x-(14)x=0的根分别为x1,x2,则( )
| A. | 0<x1x2<1 | B. | x1x2=1 | C. | 1<x1x2<2 | D. | x1x2≥2 |
 已知某三棱锥的三视图如图所示,则它的外接球体积为
已知某三棱锥的三视图如图所示,则它的外接球体积为 中,
中,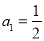 ,
,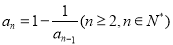 .
.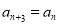 ;
;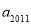 .
.