题目内容
(本小题满分12分)
四面体ABCD中,对棱AD⊥BC,对棱AB⊥CD,试证明:AC⊥BD.
四面体ABCD中,对棱AD⊥BC,对棱AB⊥CD,试证明:AC⊥BD.
略
证法1:作AO⊥平面BCD于O,则BO、CO、DO分别为AB、AC、AD在平面BCD内的射影. ∵CD⊥AB,CD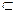 平面BCD ∴CD⊥BO(三垂线定理的逆定理)
平面BCD ∴CD⊥BO(三垂线定理的逆定理)
同理BC⊥DO ∴O为△BCD的垂心 从而BD⊥CO
∴BD⊥AC(三垂线定理),即AC⊥BD
证法2:作出向量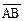 、
、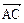 、
、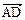 、
、 、
、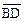 、
、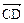 .
.
∵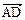 ⊥
⊥ ,
,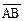 ⊥
⊥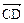
∴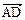 ·
· =0,
=0,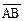 ·
·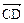 =0
=0
又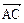 =
=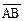 +
+ ,
,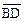 =
= +
+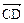
∴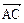 ·
·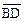 =
=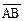 ·
· +
+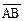 ·
·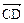 +
+
 +
+ ·
·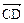
=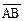 ·
·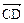 +
+ (
(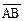 +
+ +
+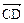 )
)
=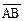 ·
·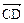 +
+ ·
·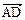 =0
=0
∴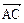 ⊥
⊥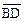 ∴AC⊥BD
∴AC⊥BD
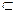 平面BCD ∴CD⊥BO(三垂线定理的逆定理)
平面BCD ∴CD⊥BO(三垂线定理的逆定理)同理BC⊥DO ∴O为△BCD的垂心 从而BD⊥CO
∴BD⊥AC(三垂线定理),即AC⊥BD
证法2:作出向量
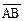 、
、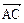 、
、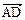 、
、 、
、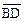 、
、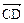 .
.∵
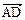 ⊥
⊥ ,
,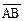 ⊥
⊥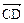
∴
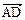 ·
· =0,
=0,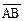 ·
·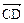 =0
=0又
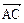 =
=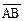 +
+ ,
,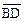 =
= +
+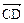
∴
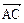 ·
·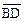 =
=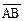 ·
· +
+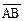 ·
·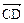 +
+
 +
+ ·
·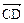
=
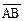 ·
·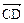 +
+ (
(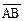 +
+ +
+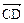 )
)=
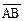 ·
·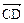 +
+ ·
·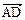 =0
=0∴
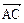 ⊥
⊥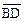 ∴AC⊥BD
∴AC⊥BD
练习册系列答案
相关题目
 表示平面,
表示平面, 表示直线,给定下列四个命题:
表示直线,给定下列四个命题: ; ②
; ② ;
; ; ④
; ④ .
.
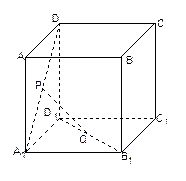
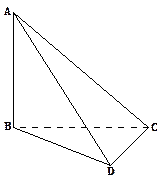
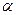 、
、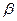 和两条不重合的直线,m、n,有下列四个命题
和两条不重合的直线,m、n,有下列四个命题 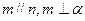 ,则
,则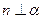 ②若
②若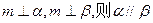
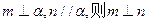 ④若
④若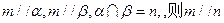
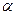 、
、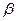 ,直线
,直线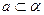 ,则“
,则“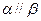 ”是“直线
”是“直线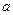
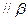 ”的( )
”的( )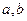 表示直线,
表示直线,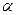 表示平面):①若
表示平面):①若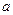 //
//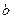 ,
,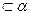 ,则
,则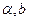 //
//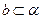 ,则
,则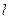 ⊥平面
⊥平面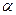 内所有直线”的充要条件是“
内所有直线”的充要条件是“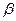 ”的必要不充分条件是“
”的必要不充分条件是“