题目内容
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C, AB=3,BC=5.
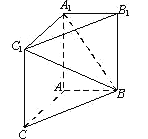
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)求点C到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)第(1)问,直接转化成平面ABC⊥平面AA1C1C. (2)利用空间向量法求二面角A1-BC1-B1的余弦值. (3)利用空间向量法求点C到平面![]() 的距离.
的距离.
试题解析:
证明:(1)因为![]() 为正方形,所以
为正方形,所以![]() .
.
因为平面ABC⊥平面AA1C1C,且平面ABC![]() 平面AA1C1C
平面AA1C1C ![]() ,所以
,所以![]() ⊥平面ABC.
⊥平面ABC.
(2)由(1)知, ![]() ⊥AC,
⊥AC, ![]() ⊥AB.
⊥AB.
由题意知![]() ,所以
,所以![]() .
.
如图,以A为原点建立空间直角坐标系![]() ,则
,则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
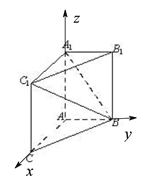
,则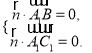 即
即![]()
令![]() ,则
,则![]() ,所以
,所以![]() .
.
同理可得,平面![]() 的法向量为
的法向量为![]() .
.
所以![]() .
.
由题知二面角A1-BC1-B1为锐角,所以二面角A1-BC1-B1的余弦值为![]() .
.
(3)由(2)知平面![]() 的法向量为
的法向量为![]() ,
, ![]()
所以点C到平面![]() 距离
距离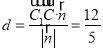 .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
【题目】把单位正方体的六个面分别染上6种颜色,并画上个数不同的金鸡,各面的颜色与鸡的个数对应如表:
面上所染颜色 | 红 | 黄 | 蓝 | 青 | 紫 | 绿 |
该面上的金鸡个数 | 1 | 2 | 3 | 4 | 5 | 6 |
取同样的4个上述的单位正方体拼成一个如图所示的水平放置的长方体.则这个长方体的下底面总计画有______个金鸡