题目内容
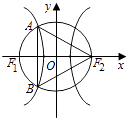
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,椭圆
,椭圆![]() 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]()
![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() (0,1),且
(0,1),且![]() =
=![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)由椭圆![]() 上任意一点到椭圆两个焦点的距离之和为
上任意一点到椭圆两个焦点的距离之和为![]() 可得
可得![]() ,由
,由![]() 的焦距为
的焦距为![]() ,可得
,可得![]() ,再由
,再由![]() 的关系可得
的关系可得![]() ,进而得到椭圆方程;(II)直线
,进而得到椭圆方程;(II)直线![]() 代入椭圆方程,运用韦达定理和判别式大于
代入椭圆方程,运用韦达定理和判别式大于![]() ,再由中点坐标公式和两直线垂直的条件,可得
,再由中点坐标公式和两直线垂直的条件,可得![]() 的方程,解方程可得
的方程,解方程可得![]() ,从而可得直线方程.
,从而可得直线方程.
试题解析:(Ⅰ)由已知![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,
,
所以![]() ,
,
所以椭圆C的方程为![]() 。
。
(Ⅱ)由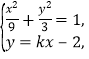 得
得![]() ,
,
直线与椭圆有两个不同的交点,所以![]() 解得
解得![]() 。
。
设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() )
)
则![]() ,
,![]() ,
,
计算![]() ,
,
所以,A,B中点坐标E(![]() ,
,![]() ),
),
因为![]() =
=![]() ,所以PE⊥AB,
,所以PE⊥AB,![]() ,
,
所以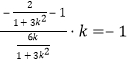 , 解得
, 解得![]() ,
,
经检验,符合题意,所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.

练习册系列答案
相关题目
【题目】已知某海滨浴场海浪的高度y(米)是时间t(0≤t≤24,单位:时)的函数,记作:![]() .下表是某日各时的浪高数据.
.下表是某日各时的浪高数据.
t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求函数y=f(t)的函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?