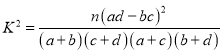题目内容
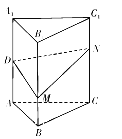
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 是边
是边![]() 的中点.平面
的中点.平面![]() 平面
平面![]() ,
,![]() ,
,![]() .线段
.线段![]() 上的点
上的点![]() 满足
满足![]() .
.
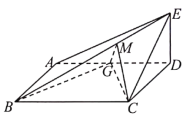
(1)证明:![]() 面
面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析 (2)![]()
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,根据相似三角形和比例关系,证得
,根据相似三角形和比例关系,证得![]() ,再利用线面平行的判定定理,即可证得
,再利用线面平行的判定定理,即可证得![]() 平面
平面![]() ;
;
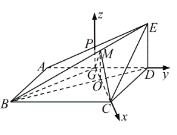
(2)以![]() 为坐标原点,
为坐标原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系,得到向量
轴建立空间直角坐标系,得到向量![]() 和平面
和平面![]() 的法向量
的法向量![]() ,利用向量的夹角公式,即可求解.
,利用向量的夹角公式,即可求解.
(1)证明:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
因为![]() 是菱形,且
是菱形,且![]() 是
是![]() 的中点,所以
的中点,所以![]() ,且
,且![]() ,
,
又由已知![]() ,于是
,于是![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)作![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,知
,知![]() 在平面
在平面![]() 内.
内.
又由题知,![]() ,于是
,于是![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() ,
,![]() ,
,
在菱形![]() 中,
中,![]() ,所以
,所以![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系,不妨设
轴建立空间直角坐标系,不妨设![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() 为正三角形,
为正三角形,![]() ,
,
于是![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
由![]() ,且
,且![]() ,可得
,可得![]() ,故
,故![]() ,
,
由![]() ,
,![]() 知
知![]() 平面
平面![]() ,
,
所以![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则![]() ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

【题目】3月底,我国新冠肺炎疫情得到有效防控,但海外确诊病例却持续暴增,防疫物资供不应求,某医疗器械厂开足马力,日夜生产防疫所需物品.已知该厂有两条不同生产线![]() 和
和![]() 生产同一种产品各10万件,为保证质量,现从各自生产的产品中分别随机抽取20件,进行品质鉴定,鉴定成绩的茎叶图如下所示:
生产同一种产品各10万件,为保证质量,现从各自生产的产品中分别随机抽取20件,进行品质鉴定,鉴定成绩的茎叶图如下所示:

该产品的质量评价标准规定:鉴定成绩达到![]() 的产品,质量等级为优秀;鉴定成绩达到
的产品,质量等级为优秀;鉴定成绩达到![]() 的产品,质量等级为良好;鉴定成绩达到
的产品,质量等级为良好;鉴定成绩达到![]() 的产品,质量等级为合格.
的产品,质量等级为合格.
(1)从等级为优秀的样本中随机抽取两件,求两件均由![]() 生产线生产的概率;
生产线生产的概率;
(2)请完成下面质量等级与生产线产品列联表,并判断能不能在误差不超过0.05的情况下,认为产品等级是否达到良好以上与生产产品的生产线有关.
|
| 合计 | |
良好以上 | |||
合格 | |||
合计 |
附: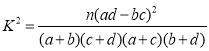
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |