Question

【题目】已知f(x)＝|2x＋4|＋|x－3|.

(1)解关于x的不等式f(x)<8；

(2)对于正实数a，b，函数g(x)＝f(x)－3a－4b只有一个零点，求的最小值.

Answer 1

【答案】（1）(－3，1)；（2）.

【解析】

（1）将函数解析式化成分段函数，用分类讨论的方法解不等式.

（2）作出函数的大致图象，的零点，转化为函数与的交点，由图可知，然后利用基本不等式求的最小值.

解：（1）由题意可得,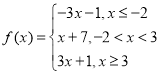

故当时，不等式可化为，解得，故此时不等式的解集为；

当时，不等式可化为，解得，故此时不等式的解集为；

当时，不等式可化为，解得，此时不等式无解,

综上，不等式的解集为.

(2)作出函数的大致图象及直线，如图.

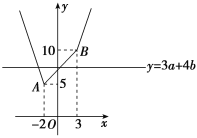
由图可知，当只有一个零点时，，

即，

故

,

当且仅当时等号成立．

的最小值为.