题目内容
【题目】设![]() ,函数
,函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 上有唯一零点,试求a的值.
上有唯一零点,试求a的值.
【答案】(1)![]() 的单调减区间是
的单调减区间是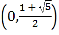 ,单调增区间是
,单调增区间是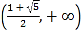 ;(2)
;(2)![]() .
.
【解析】
(1)将![]() 代入
代入![]() 中可得
中可得![]() (
(![]() ),令
),令![]() ,解得
,解得![]() ,进而求得单调区间;
,进而求得单调区间;
(2)令![]() ,解得
,解得![]() (舍),
(舍),![]() ,可得函数
,可得函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,则
上单调递增,则![]() ,由于函数
,由于函数![]() 在区间
在区间![]() 上有唯一零点,则
上有唯一零点,则![]() ,整理即为
,整理即为![]() ,设
,设![]() ,可得
,可得![]() 在
在![]() 是单调递增的,则
是单调递增的,则![]() ,进而求得
,进而求得![]()
(1)函数![]() ,
,
当![]() 时,
时,![]() (
(![]() ),
),
∴![]() ,
,
令![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
∴ 时,
时,![]() ;
;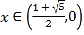 时,
时,![]() ,
,
∴![]() 的单调减区间是
的单调减区间是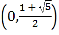 ,单调增区间是
,单调增区间是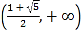
(2)![]() ,
,
则![]() ,
,
令![]() ,得
,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴方程的解为![]() (舍),
(舍),![]() ;
;
∴函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,
,
若函数![]() 在区间
在区间![]() 上有唯一零点,
上有唯一零点,
则![]() ,
,
而![]() 满足
满足![]() ,
,
∴![]() ,
,
即![]() ,
,
设![]() ,
,
∵![]() 在
在![]() 是单调递增的,
是单调递增的,
∴![]() 至多只有一个零点,
至多只有一个零点,
而![]() ,
,
∴用![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]()

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目