题目内容
6．用反证法证明命题：“若a＞0，b＞0，a3+b3=2，则a+b≤2”时，反设正确的是（ ）| A． | a+b≤2 | B． | a+b＜2 | C． | a+b≥2 | D． | a+b＞2 |
分析 “a+b≤2”的否定是“a+b＞2”，由此可得结论．
解答 解：∵“a+b≤2”的否定是“a+b＞2”，
∴用反证法证明命题：“若a＞0，b＞0，a3+b3=2，则a+b≤2”时，反设是“a+b＞2”．
故选：D．
点评 本题考查反证法，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
16．已知x∈R，命题p：x＞0，命题q：x+sinx＞0，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
17．记集合A={x|$\frac{1}{x-1}$＜1}，B={x|（x-1）（x+a）＞0}，若x∈A是x∈B的充分不必要条件，则实数a的取值范围是（ ）
| A． | （-2，-1] | B． | [-2，-1] | C． | ∅ | D． | [-2，+∞） |
14．
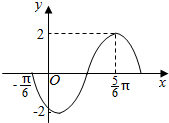已知函数f（x）=2sin（ωx+φ），（ω＞0，0＜φ＜2π）的部分图象如图所示，则f（x）的表达式为（ ）
已知函数f（x）=2sin（ωx+φ），（ω＞0，0＜φ＜2π）的部分图象如图所示，则f（x）的表达式为（ ）| A． | $f（x）=2sin（\frac{4}{3}x+\frac{2}{9}π）$ | B． | $f（x）=2sin（\frac{4}{3}x+\frac{25}{18}π）$ | ||
| C． | $f（x）=2sin（\frac{3}{2}x+\frac{π}{4}）$ | D． | $f（x）=2sin（\frac{3}{2}x+\frac{5}{4}π）$ |
如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC．
18．函数y=$\frac{1}{3}{x^3}-{x^2}$的单调递减区间是（ ）
| A． | （-∞，0） | B． | （-∞，2） | C． | （2，+∞） | D． | （0，2） |
15．从同一顶点出发的三条棱长分别为1、1、$\sqrt{2}$的长方体的各顶点均在同一个球面上，则该球的体积为 （ ）
| A． | $\frac{32π}{3}$ | B． | 4π | C． | 2π | D． | $\frac{4π}{3}$ |
