题目内容
14.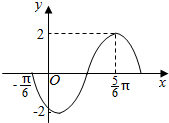 已知函数f(x)=2sin(ωx+φ),(ω>0,0<φ<2π)的部分图象如图所示,则f(x)的表达式为( )
已知函数f(x)=2sin(ωx+φ),(ω>0,0<φ<2π)的部分图象如图所示,则f(x)的表达式为( )| A. | $f(x)=2sin(\frac{4}{3}x+\frac{2}{9}π)$ | B. | $f(x)=2sin(\frac{4}{3}x+\frac{25}{18}π)$ | ||
| C. | $f(x)=2sin(\frac{3}{2}x+\frac{π}{4})$ | D. | $f(x)=2sin(\frac{3}{2}x+\frac{5}{4}π)$ |
分析 根据函数的图象,由周期求出ω,由五点法作图求出φ的值,可得函数f(x)的解析式.
解答 解:由函数的图象可得$\frac{3}{4}$T=$\frac{3}{4}$•$\frac{2π}{ω}$=$\frac{5π}{6}$+$\frac{π}{6}$,∴ω=$\frac{3}{2}$.
再根据五点法作图可得 $\frac{3}{2}$(-$\frac{π}{6}$)+φ=π,求得φ=$\frac{5π}{4}$,∴f(x)=2sin($\frac{3}{2}$x+$\frac{5π}{4}$),
故选:D.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
相关题目
9.已知函数f(x)=sin(2x+θ)+$\sqrt{3}$ cos(2x+θ)(x∈R)满足2015f(-x)=$\frac{1}{{{{2015}^{f(x)}}}}$,且f(x)在[0,$\frac{π}{4}$]上是减函数,则θ的一个可能值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
19.已知集合M={a,b,c},集合A={x|x⊆M},则集合A有几个元素( )
| A. | 3 | B. | 6 | C. | 7 | D. | 8 |
6.用反证法证明命题:“若a>0,b>0,a3+b3=2,则a+b≤2”时,反设正确的是( )
| A. | a+b≤2 | B. | a+b<2 | C. | a+b≥2 | D. | a+b>2 |