题目内容
1. 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.(Ⅰ)求证:PC⊥AB
(Ⅱ)设点E为棱PA的中点,求三棱锥P-EBC的体积.
分析 (Ⅰ)根据图形得出PD⊥AB.CD⊥AB,即可判断AB⊥平面PCD.得证PC⊥AB
(Ⅱ)转化VP-ABC=$\frac{1}{3}×\frac{1}{2}×2×2×2$,求解即可.
解答 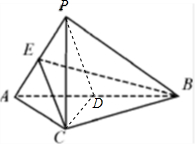 (Ⅰ)证明:取AB中点D,连结PD,CD
(Ⅰ)证明:取AB中点D,连结PD,CD
∵AP=BP,
∴PD⊥AB.
∵AC=BC.
∴CD⊥AB.
∵PD∩CD=D.
∴AB⊥平面PCD.
∵PC?平面PCD,
∴PC⊥AB;
(Ⅱ)解:在Rt△ABC中,AC=BC=2
∴AB=2$\sqrt{2}$,
在Rt△PDB中,PB=2$\sqrt{2}$,BD=$\sqrt{2}$
PD=$\sqrt{P{B}^{2}-B{D}^{2}}$=$\sqrt{6}$,
又∵PC⊥AC,PC⊥AB,AB∩AC=A
∴PC⊥平面ABC
∴PC⊥CD
∴PC=$\sqrt{P{D}^{2}-C{D}^{2}}$=2,
∴VP-ABC=$\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{4}{3}$
∵点E为棱PA的中点,
∴三棱锥P-EBC的体积V=$\frac{2}{3}$.
点评 本题考查了空间几何体的体积计算,空间直线与直线的位置关系,属于中档题.

练习册系列答案
相关题目
12.命题:?x∈R,x>0的否定为( )
| A. | ?x∈R,x≤0 | B. | ?x0∈R,x0>0 | C. | ?x0∈R,x0≤0 | D. | ?x∈R,x<0 |
9.已知函数f(x)=sin(2x+θ)+$\sqrt{3}$ cos(2x+θ)(x∈R)满足2015f(-x)=$\frac{1}{{{{2015}^{f(x)}}}}$,且f(x)在[0,$\frac{π}{4}$]上是减函数,则θ的一个可能值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
6.用反证法证明命题:“若a>0,b>0,a3+b3=2,则a+b≤2”时,反设正确的是( )
| A. | a+b≤2 | B. | a+b<2 | C. | a+b≥2 | D. | a+b>2 |
11.已知角α,β均为锐角,且cosα=$\frac{3}{5}$,tan(α-β)=-$\frac{1}{3}$,tanβ=( )
| A. | $\frac{1}{3}$ | B. | $\frac{9}{13}$ | C. | $\frac{13}{9}$ | D. | 3 |