题目内容
给出问题:设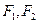 是双曲线
是双曲线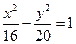 的焦点,点
的焦点,点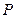 是双曲线上的动点,点
是双曲线上的动点,点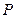 到焦点
到焦点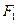 的距离等于
的距离等于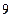 ,求点
,求点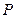 到
到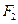 的距离,某同学的解答如下:双曲线的实轴长为
的距离,某同学的解答如下:双曲线的实轴长为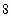 ,由
,由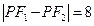 即
即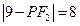 ,得
,得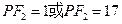 。试问该同学的解答是否正确?若正确,请说明依据,若不正确,请说明理由。
。试问该同学的解答是否正确?若正确,请说明依据,若不正确,请说明理由。
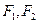 是双曲线
是双曲线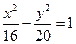 的焦点,点
的焦点,点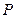 是双曲线上的动点,点
是双曲线上的动点,点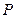 到焦点
到焦点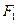 的距离等于
的距离等于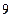 ,求点
,求点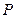 到
到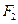 的距离,某同学的解答如下:双曲线的实轴长为
的距离,某同学的解答如下:双曲线的实轴长为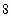 ,由
,由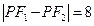 即
即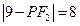 ,得
,得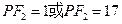 。试问该同学的解答是否正确?若正确,请说明依据,若不正确,请说明理由。
。试问该同学的解答是否正确?若正确,请说明依据,若不正确,请说明理由。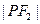 根本不可能为
根本不可能为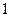 ,而只能为
,而只能为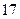 。
。由定义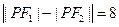 ,双曲线
,双曲线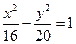 中,
中,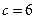 ,
,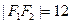 ,∴
,∴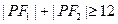 ,当
,当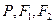 在同一直线上时取得“=”号,由
在同一直线上时取得“=”号,由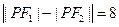 得
得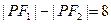 ,
,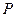 在双曲线的左右支上时,
在双曲线的左右支上时,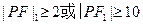 ,同理,
,同理,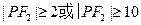 ,因此,
,因此,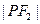 根本不可能为
根本不可能为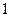 ,而只能为
,而只能为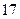 。
。
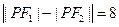 ,双曲线
,双曲线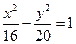 中,
中,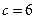 ,
,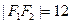 ,∴
,∴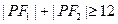 ,当
,当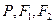 在同一直线上时取得“=”号,由
在同一直线上时取得“=”号,由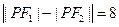 得
得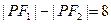 ,
,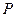 在双曲线的左右支上时,
在双曲线的左右支上时,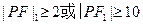 ,同理,
,同理,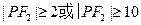 ,因此,
,因此,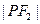 根本不可能为
根本不可能为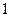 ,而只能为
,而只能为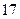 。
。
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目

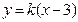 与双曲线
与双曲线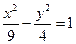 只有一个公共点,则
只有一个公共点,则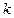 的值有( )
的值有( )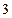 个
个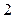 个
个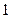 个
个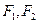 是双曲线的两个焦点,
是双曲线的两个焦点,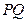 是过点
是过点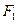 且垂直于实轴所在直线的双曲线的弦,
且垂直于实轴所在直线的双曲线的弦,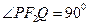 ,则双曲线的离心率为( )
,则双曲线的离心率为( )



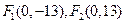 的距离的差的绝对值等于
的距离的差的绝对值等于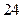 的点的轨迹是( )
的点的轨迹是( )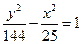
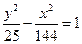

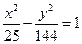
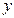 轴上,且
轴上,且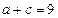 ,
,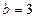 ,则它的标准方程为 。
,则它的标准方程为 。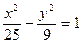
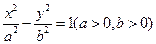 的离心率
的离心率 ,虚半轴长为
,虚半轴长为 ,求双曲线的方程。
,求双曲线的方程。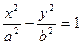 上一点,
上一点,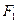 为一个焦点,以
为一个焦点,以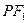 为直径的圆与圆
为直径的圆与圆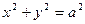 的位置关系为 ( )
的位置关系为 ( ) 内切 B
内切 B