题目内容
已知双曲线E的中心为原点,P(3,0)是E的焦点,过P的直线l与E相交于A,B两点,且AB的中点为N(-12,-15),则E的方程式为( )
A.
| B.
| C.
| D.
|
由已知条件易得直线l的斜率为k=kFN=1,
设双曲线方程为
-
=1,
A(x1,y1),B(x2,y2),
则有
,
两式相减并结合x1+x2=-24,y1+y2=-30得
=
,
从而=
=1
即4b2=5a2,
又a2+b2=9,
解得a2=4,b2=5,
故选B.
设双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
A(x1,y1),B(x2,y2),
则有
|
两式相减并结合x1+x2=-24,y1+y2=-30得
| y1-y2 |
| x1-x2 |
| 4b2 |
| 5a2 |
从而=
| 4b2 |
| 5a2 |
即4b2=5a2,
又a2+b2=9,
解得a2=4,b2=5,
故选B.

练习册系列答案
相关题目
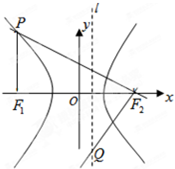
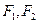 是双曲线
是双曲线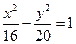 的焦点,点
的焦点,点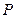 是双曲线上的动点,点
是双曲线上的动点,点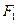 的距离等于
的距离等于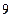 ,求点
,求点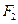 的距离,某同学的解答如下:双曲线的实轴长为
的距离,某同学的解答如下:双曲线的实轴长为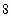 ,由
,由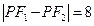 即
即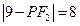 ,得
,得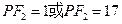 。试问该同学的解答是否正确?若正确,请说明依据,若不正确,请说明理由。
。试问该同学的解答是否正确?若正确,请说明依据,若不正确,请说明理由。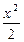 -y2=1有公共渐近线的双曲线方程是
-y2=1有公共渐近线的双曲线方程是 -
- ="1"
="1"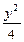 -
-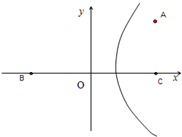
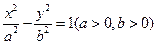 的一个焦点为F,左右顶点分别为A,B .P是双曲线上任意一点,则分别以线段
的一个焦点为F,左右顶点分别为A,B .P是双曲线上任意一点,则分别以线段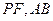 为直径的两圆的位置关系为
为直径的两圆的位置关系为