题目内容

5．如图，曲线y=f（x）在点P（5，f（5））处的切线方程是y=ax+8，若f（5）+f′（5）=2，则实数a=-1．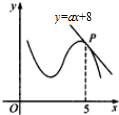

分析 由题意求得f′（5）=a，f（5）=5a+8，代入f（5）+f′（5）=2，求得a的值．

解答 解：因为曲线y=f（x）在点P（5，f（5））处的切线方程是y=ax+8，
所以f′（5）=a，f（5）=5a+8，
由f（5）+f′（5）=2，得a+5a+8=2，解得：a=-1．
故答案为：-1．

点评 本题考查了利用导数研究过曲线上某点处的切线方程，过曲线上某点的切线的斜率，就是函数在该点处的导数值，是中档题．

练习册系列答案
相关题目
5．已知函数f（x）=2x-2-x，若f（a）=3，求f（2a）的值．
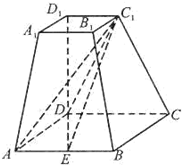16．如图，在四棱台ABCD-A1B1C1D1中，DD1⊥底面ABCD，四边形ABCD为正方形，DD1=AD=2，A1B1=1，C1E∥平面ADD1A1．
（Ⅰ）证明：E为AB的中点；
（Ⅱ）求点E到平面ADC1的距离．
13．设函数f（x）=mx2-2mlnx-6+m，g（x）=x2-lnx
（1）当m=1时，求函数f（x）的单调区间及极值；
（2）若对于x∈[1，3]，f（x）＜0恒成立，求实数m的取值范围；
（3）若m＞0且对于任意x1∈[1，e]，任意x2∈[1，e]，不等式f（x1）＞g（x2）恒成立，求实数m的取值范围．
20．已知函数f（x）=lnx，g（x）+f（x）=$\frac{1}{2}$px2-qx，函数g（x）的图象在点（1，g（1））处的切线平行于x轴．
（1）试用含有p的式子表示q；
（2）若p≤0，试讨论函数g（x）的单调性；
（3）当x≠1，h（x）f（x）=x2-4tx+4t2，（其中t为常数），若t∈（0，$\frac{1}{2}$），函数h（x）有三个极值点为a，b，c，且a＜b＜c．证明0＜2a＜b＜1＜c．
10．已知函数f（x）=（x-1）ex-x2．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）求函数f（x）的单调区间；
（3）求函数f（x）在区间[0，k]（k＞0）上的最大值．
17．从1到9选5个不重复数字的五位数，若五位数可以被3整除，则有用多少个符合条件的五位数？
14．已知数列{an}是正整数组成的等比数列，公比为q=2，a1a2a3…a20=250，则a2a4a6…a20的值为230．
15．设x，t满足约束条件$\left\{\begin{array}{l}{2x-y+2≥0}\\{8x-y-4≤0}\\{x≥0，y≥0}\end{array}\right.$，若目标函数z=4ax+by（a＞0，b＞0）的最大值为8，则a=$\frac{2}{3}$时，$\frac{1}{2a}$+$\frac{a}{b}$取得最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网