题目内容
20.已知函数f(x)=lnx,g(x)+f(x)=$\frac{1}{2}$px2-qx,函数g(x)的图象在点(1,g(1))处的切线平行于x轴.(1)试用含有p的式子表示q;
(2)若p≤0,试讨论函数g(x)的单调性;
(3)当x≠1,h(x)f(x)=x2-4tx+4t2,(其中t为常数),若t∈(0,$\frac{1}{2}$),函数h(x)有三个极值点为a,b,c,且a<b<c.证明0<2a<b<1<c.
分析 (1)由题意化简g(x)=-lnx+$\frac{1}{2}$px2-qx,求导g′(x)=-$\frac{1}{x}$+px-q;从而可得g′(1)=-1+p-q=0,从而解得;
(2)先确定函数g(x)=-lnx+$\frac{1}{2}$px2-qx的定义域,再求导g′(x)=-$\frac{1}{x}$+px-q=$\frac{(px+1)(x-1)}{x}$,讨论以确定其正负,从而确定函数的单调性;
(3)由题意化简h(x)=$\frac{{x}^{2}-4tx+4{t}^{2}}{lnx}$,求导h′(x)=$\frac{(x-2t)(2lnx-\frac{x-2t}{x})}{l{n}^{2}x}$,再令m(x)=2lnx-$\frac{x-2t}{x}$,求导m′(x)=$\frac{2(x-t)}{{x}^{2}}$;从而可判断0<a<t,b=2t<1,c>1;从而证明.
解答 解:(1)由已知得g(x)=-lnx+$\frac{1}{2}$px2-qx,
g′(x)=-$\frac{1}{x}$+px-q,
又∵函数g(x)的图象在点(1,g(1))处的切线平行于x轴,
∴g′(1)=-1+p-q=0,
故q=p-1;
(2)由(1)知,g(x)=-lnx+$\frac{1}{2}$px2-qx的定义域为(0,+∞),
g′(x)=-$\frac{1}{x}$+px-q=$\frac{(px+1)(x-1)}{x}$,
①当p=0时,
g(x)在(0,1)上是减函数,在(1,+∞)上是增函数;
②当p=-1时,g′(x)=-$\frac{(x-1)^{2}}{x}$≤0,
故g(x)在(0,+∞)上是减函数;
③当p<-1时,g′(x)=$\frac{p(x+\frac{1}{p})(x-1)}{x}$;
0<-$\frac{1}{p}$<1;
故g(x)在(0,-$\frac{1}{p}$),(1,+∞)上是减函数,在(-$\frac{1}{p}$,1)上是增函数;
④当-1<p<0时,g′(x)=$\frac{p(x+\frac{1}{p})(x-1)}{x}$;
-$\frac{1}{p}$>1;
故g(x)在(0,1),(-$\frac{1}{p}$,+∞)上是减函数,在(1,-$\frac{1}{p}$)上是增函数;
(3)证明:由题意得,
h(x)=$\frac{{x}^{2}-4tx+4{t}^{2}}{lnx}$,h′(x)=$\frac{(x-2t)(2lnx-\frac{x-2t}{x})}{l{n}^{2}x}$
令m(x)=2lnx-$\frac{x-2t}{x}$,m′(x)=$\frac{2(x-t)}{{x}^{2}}$;
故m(x)=2lnx-$\frac{x-2t}{x}$在(0,t)上单调递减,在(t,+∞)上单调递增;
而函数h(x)有三个极值点为a,b,c,
则m(x)=2lnx-$\frac{x-2t}{x}$=0在(0,+∞)上有两个不相等相都不等于2t的根,
且h(x)的一个极值点为2t;
∵t∈(0,$\frac{1}{2}$),mmin(x)=m(t)=2lnt+1<2ln$\frac{1}{2}$+1<0;
m(1)=2ln1+2t-1=2t-1<0;
又∵a<b<c,
∴0<a<t,b=2t<1,c>1;
∴0<2a<b<1<c.
点评 本题考查了导数的综合应用及分类讨论的思想应用,难题在于构造函数以使问题简化,属于难题.

 阅读快车系列答案
阅读快车系列答案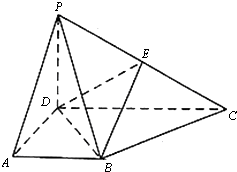 已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,AD⊥AB,AD=AB=$\frac{1}{2}$CD=1,PD⊥面ABCD,PD=$\sqrt{2}$,E是PC的中点
已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,AD⊥AB,AD=AB=$\frac{1}{2}$CD=1,PD⊥面ABCD,PD=$\sqrt{2}$,E是PC的中点
 如图,已知AD是△ABC的对角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.
如图,已知AD是△ABC的对角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.