题目内容
15.设x,t满足约束条件$\left\{\begin{array}{l}{2x-y+2≥0}\\{8x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=4ax+by(a>0,b>0)的最大值为8,则a=$\frac{2}{3}$时,$\frac{1}{2a}$+$\frac{a}{b}$取得最小值.分析 作出不等式组对应的平面区域,利用线性规划求出最优解,结合基本不等式求解即可.
解答 解:作出不等式组对应的平面区域如图:
由z=4ax+by得y=-$\frac{4a}{b}$x+$\frac{z}{b}$,
∵a>0,b>0,
∴目标函数的斜率k=-$\frac{4a}{b}$<0,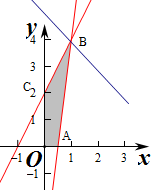
平移直线y=-$\frac{4a}{b}$x+$\frac{z}{b}$,由图象知当直线y=-$\frac{4a}{b}$x+$\frac{z}{b}$,经过点B时,直线的截距最大,此时z最大为8,
由$\left\{\begin{array}{l}{2x-y+2=0}\\{8x-y-4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,即B(1,4),
此时4a+4b=8,即$\frac{a}{2}$+$\frac{b}{2}$=1,
则$\frac{1}{2a}$+$\frac{a}{b}$=$\frac{\frac{a}{2}+\frac{b}{2}}{2a}$+$\frac{a}{b}$=$\frac{1}{4}$+$\frac{b}{4a}$+$\frac{a}{b}$≥$\frac{1}{4}$+2$\sqrt{\frac{b}{4a}•\frac{a}{b}}$=$\frac{1}{4}$+1=$\frac{5}{4}$,
当且仅当$\frac{b}{4a}$=$\frac{a}{b}$,即b=2a时取得号,
∵4a+4b=8,
∴4a+8a=8,
解得a=$\frac{8}{12}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,训练了基本不等式的应用,是中档题.

| A. | f(x)=-x3 | B. | f(x)=$\sqrt{-x}$ | C. | f(x)=-tanx | D. | f(x)=$\frac{1}{x}$ |
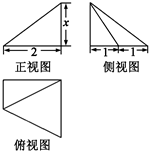
| A. | 2 | B. | 3 | C. | $\frac{4}{15}$ | D. | $\frac{4}{5}$ |
| A. | (-∞,2] | B. | (2,+∞) | C. | (-∞,1] | D. | (-∞,0)∪[1,+∞) |
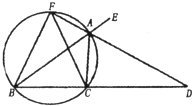 如图,已知AD是△ABC的对角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.
如图,已知AD是△ABC的对角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.