题目内容
18．已知（1+i）2=a+bi（a，b∈R，i为虚数单位），则a+b=2．分析 通过题意直接计算即可．
解答 解：（1+i）2=1+2i+i2=2i，
∵（1+i）2=a+bi（a，b∈R，i为虚数单位），
∴$\left\{\begin{array}{l}{a=0}\\{b=2}\end{array}\right.$，
∴a+b=2，
故答案为：2．
点评 本题考查复数的相关知识，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
13．为了得到函数y=$\frac{1}{2}$cos2x的图象，可以把函数y=$\frac{1}{2}$sin（2x+$\frac{π}{3}$）的图象上所有的点（ ）
| A． | 向右平移$\frac{π}{12}$个单位 | B． | 向右平移$\frac{π}{6}$个单位 | ||
| C． | 向左平移$\frac{π}{12}$个单位 | D． | 向左平移$\frac{π}{6}$个单位 |
3．已知某几何体的三视图如图所示，则该几何体的外接球的表面积为（ ）
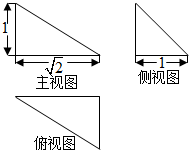
| A． | π | B． | 2π | C． | 3π | D． | 4π |
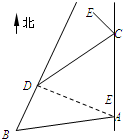如图，甲船从A处以每小时30海里的速度沿正北方向航行，乙船在B处沿固定方向匀速航行，B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处．当甲船航行20分钟到达C处时，乙船航行到甲船的北偏西120°方向的D处，此时两船相距10海里．
8．若过点（2，0）的直线l与圆C：x2+y2=1有公共点，则直线l的斜率k的取值范围是（ ）
| A． | [-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$] | B． | （-∞，-$\frac{\sqrt{3}}{3}$]∪[$\frac{\sqrt{3}}{3}$，+∞） | C． | $[{-\sqrt{3}，\sqrt{3}}]$ | D． | $（{-∞，-\sqrt{3}}]∪[{\sqrt{3}，+∞}）$ |