题目内容
6.已知函数y=sin(x+φ)(|φ|<$\frac{π}{2}$)的图象与x轴的一个交点是(-$\frac{8π}{3}$,0),试求这个函数的解析式.分析 由题意可得-$\frac{8π}{3}$+φ=kπ,k∈z;再结合|φ|<$\frac{π}{2}$,可得φ 的值,从而得到函数y的解析式.
解答 解:由题意可得-$\frac{8π}{3}$+φ=kπ,k∈z,∴φ=kπ+$\frac{3π}{8}$,k∈z.
再结合|φ|<$\frac{π}{2}$,可得φ=$\frac{3π}{8}$,函数y=sin(x+$\frac{3π}{8}$).
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,根据函数的零点求φ的值,属于基础题.

练习册系列答案
相关题目
16.执行如图所示的程序框图,结果是( )
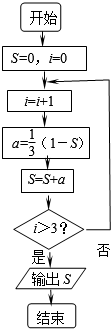

| A. | $\frac{65}{81}$ | B. | $\frac{19}{27}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
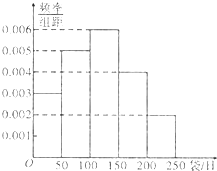 如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立. 如图,BD是四边形ABCD的外接圆⊙O的直径,PA⊥平面ABCD,E为PD的中点,已知∠ABD=∠CBD=60°,PA=BD=2.
如图,BD是四边形ABCD的外接圆⊙O的直径,PA⊥平面ABCD,E为PD的中点,已知∠ABD=∠CBD=60°,PA=BD=2.