题目内容
5.对于任意实数x,记[x]表示不超过x的最大整数,{x}=x-[x],[x]表示不小于x的最小整数,若x1,x2,…,xm(0≤x1<x2<…<xm≤6)是区间[0,6]中满足方程[x]•{x}•[x]=1的一切实数,则x1+x2+…+xm的值是$\frac{95}{6}$.分析 根据新定义,[x]表示不超过x的最大整数,{x}=x-[x],需要分类讨论,根据条件得到x=a+$\frac{1}{a(a+1)}$,继而求出a的可能值,最后代入计算即可.
解答 解:显然,x不可能是整数,否则由于{x}=0,方程[x]•{x}•],x=1不可能成立.设[x]=a,
则{x}=x-a,x=a+1,代入得a(x-a)(a+1)=1,解得x=a+$\frac{1}{a(a+1)}$.
考虑到x∈[0,6],且[x]≠0,所以a=1,2,3,4,5,故符合条件的解有5个,即m=5,
则x1+x2+…+xm=x1+x2+…+x5=$\frac{5(5+1)}{2}$+1-$\frac{1}{5+1}$=$\frac{95}{6}$,
故答案为:$\frac{95}{6}$.
点评 本题考查了函数的值,需要分类进行讨论,新定义一般需要认真读题,理解题意,灵活利用已知定义,属于中档题.

练习册系列答案
相关题目
16.执行如图所示的程序框图,若a=7.则输出的S=( )
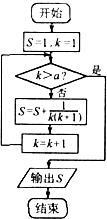

| A. | $\frac{6}{7}$ | B. | $\frac{15}{8}$ | C. | $\frac{13}{7}$ | D. | $\frac{11}{6}$ |
20.函数y=ax+1-3(a>0,a≠1)过定点A,若点A在直线mx+ny=-2(m>0,n>0)上,则$\frac{1}{m}$+$\frac{1}{n}$的最小值为( )
| A. | 3 | B. | 2$\sqrt{2}$ | C. | $\frac{3+2\sqrt{2}}{2}$ | D. | $\frac{3-2\sqrt{2}}{3}$ |
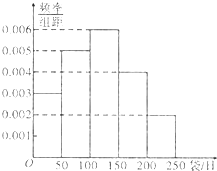 如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.