题目内容
【题目】已知椭圆C:![]() 1(a>b>0),椭圆上的点到焦点的最小距离为
1(a>b>0),椭圆上的点到焦点的最小距离为![]() 且过点P(
且过点P(![]() ,1).
,1).
(1)求椭圆C的方程;
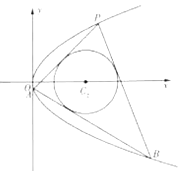
(2)若过点M(3,0)的直线l与椭圆C有两个不同的交点P和Q,若点P关于x轴的对称点为P',判断直线P'Q是否经过定点,如果经过,求出该定点坐标;如果不经过,说明理由.
【答案】(1)![]() .(2)直线P'Q过x轴上定点
.(2)直线P'Q过x轴上定点![]() .
.
【解析】
(1)利用已知条件列出方程组,求出a,b即可得到椭圆方程.
(2)分析当斜率为![]() 时可知定点若存在则必在x轴上,设定点坐标,再设直线方程与P、Q坐标,联立直线与椭圆方程,利用韦达定理,结合三点共线则任意两点的斜率相等列式,进而求出定点坐标即可.
时可知定点若存在则必在x轴上,设定点坐标,再设直线方程与P、Q坐标,联立直线与椭圆方程,利用韦达定理,结合三点共线则任意两点的斜率相等列式,进而求出定点坐标即可.
解:(1)由题意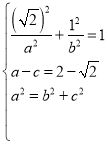 ,解得
,解得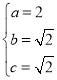 ,
,
故椭圆C的方程为![]() .
.
(2)显然直线![]() 的斜率存在,且当
的斜率存在,且当![]() 斜率为0时, 直线P'Q为x轴.
斜率为0时, 直线P'Q为x轴.
故定点若存在则必在x轴上,设定点为![]() .
.
故设![]() ,
,![]() .
.
将直线与椭圆的方程联立得: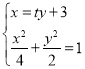 ,
,
消去![]() ,整理得
,整理得![]() .
.
由根与系数之间的关系可得:![]() ,
,![]() .
.
∵点P关于y轴的对称点为P',则P'(x1,﹣y1),且![]() 三点共线
三点共线
∴![]() ,即
,即![]() .
.
即![]() ,
,![]()
整理对![]() ,代入韦达定理有
,代入韦达定理有![]() ,即
,即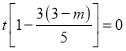 恒成立.解得
恒成立.解得![]() .
.
∴直线P'Q过x轴上定点![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目