题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平形四边形,设
是平形四边形,设![]() ,
,![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() .
.
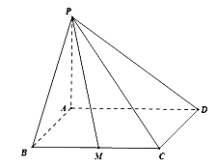
(1)若![]() ,求二面角
,求二面角![]() 的正切值;
的正切值;
(2)是否存在![]() 使
使![]() ,若存在求出
,若存在求出![]() ,若不存在请说明理由.
,若不存在请说明理由.
【答案】(1)2;(2)存在![]() ,使
,使![]() .
.
【解析】
(1)连接![]() ,由几何关系可得
,由几何关系可得![]() 是二面角
是二面角![]() 的平面角,据此可求得二面角
的平面角,据此可求得二面角![]() 的正切值.
的正切值.
(2)假设存在![]() ,使
,使![]() ,
,![]() ,设
,设![]() ,由几何关系求得EM的长度,进一步确定角θ的值即可.
,由几何关系求得EM的长度,进一步确定角θ的值即可.
(1)连接![]() ,因为
,因为![]() 是平形四边形,
是平形四边形,
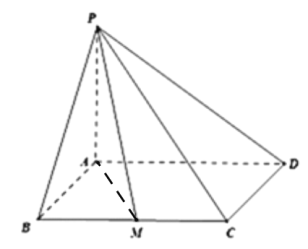
所以![]() ,
,
又![]() ,
,![]() ,由余弦定理得
,由余弦定理得![]() ,
,
所以![]() 所以
所以![]() ,即
,即![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,即二面角
,即二面角![]() 的正切值为
的正切值为![]() .
.
(2)假设存在![]() ,使
,使![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() .
.
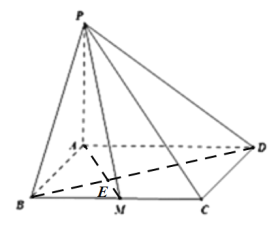
设![]() 在平行四边形
在平行四边形![]() 中,
中,![]() ,
,![]() ,
,
所以![]() .
.
设![]() ,则
,则![]() ,由
,由![]() 得
得![]() 解得
解得![]() ,故
,故![]() ,
,
所以![]() ,又
,又![]() ,
,![]() 所以有
所以有![]() ,故
,故![]() ,
,
即存在![]() ,使
,使![]() .
.

练习册系列答案
相关题目
【题目】某研究所计划利用“神舟十一号”飞船进行新产品搭载实验,计划搭载新产品![]() ,要根据该产品的研制成本、产品质量、搭载实验费用和预计产生收益来决定具体安排,通过调查,搭载每件产品有关数据如表:
,要根据该产品的研制成本、产品质量、搭载实验费用和预计产生收益来决定具体安排,通过调查,搭载每件产品有关数据如表:
因素 | 产品 | 产品 | 备注 |
研制成本、搭载费用之和/万元 | 20 | 30 | 计划最大投资 |
金额300万元产品质量/千克 | 10 | 5 | 最大搭载 |
质量110千克预计收益/万元 | 80 | 60 | —— |
则使总预计收益达到最大时, ![]() 两种产品的搭载件数分别为( )
两种产品的搭载件数分别为( )
A. 9,4 B. 8,5 C. 9,5 D. 8,4



