题目内容
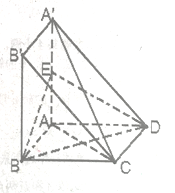
【题目】已知下图中，四边形 ABCD是等腰梯形， 
， 
， 
于M、交EF于点N， 
， 
，现将梯形ABCD沿EF折起，记折起后C、D为
、
且使
，如图示．
(Ⅰ)证明： 
平面ABFE；,
(Ⅱ)若图6中， 
，求点M到平面
的距离．
【答案】 (Ⅰ)见解析 (Ⅱ) 
．
【解析】试题分析：（I）折叠前后， 
⊥EF、MN⊥EF，故EF⊥平面
，故
.利用勾股定理可证得
，所以
平面ABFE；（II）设点M到平面
的距离为h， 
, 
，利用勾股定理证明
，利用等体积法可求得点M到平面
的距离为
.
试题解析：
(Ⅰ) 可知
，∴
⊥EF、MN⊥EF，
又
，得EF⊥平面
，
得
，
∵
∴
，
又
，∴
平面ABFE．
(Ⅱ) 设点M到平面
的距离为h，
由
，得
，①
∵
， 
，
∴
, 
,
在
中， 
，
又
， 
，得
，
∴
，
，又
，
代入①式，得
，解得
，
∴点M到平面
的距离为
．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
【题目】为了普及环保知识，增强环保意识，某校从理科甲班抽取60人，从文科乙班抽取50人参加环保知识测试．
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
（Ⅰ）根据题目完成
列联表，并据此判断是否有
的把握认为环保知识成绩优秀与学生的文理分类有关．
（Ⅱ）现已知
， 
， 
三人获得优秀的概率分别为
， 
， 
，设随机变量
表示
， 
， 
三人中获得优秀的人数，求
的分布列及期望
．
附： 
， 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
