题目内容
【题目】椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() :
:![]() 截
截![]() 轴所得的线段长等于
轴所得的线段长等于![]() .
.![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 相交于点
相交于点![]() 直线
直线![]() 分别与
分别与![]() 相交于
相交于![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,
,![]() 的面积分别为
的面积分别为![]() ,若
,若![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意可求得椭圆![]() 的方程为
的方程为![]() .直线
.直线![]() 的方程为
的方程为![]() (
(![]() 存在),
存在),![]() ,
,![]() .联立直线方程与抛物线方程可得
.联立直线方程与抛物线方程可得![]() ,,韦达定理计算可得
,,韦达定理计算可得![]() ,则
,则![]() .
.
(2)由(1)可知![]() 和
和![]() 均为直角三角形,设直线
均为直角三角形,设直线![]() 方程为
方程为![]() ,与抛物线方程联立可得
,与抛物线方程联立可得![]() ,同理可得
,同理可得![]() ,则
,则![]() .同理求得
.同理求得![]() ,则
,则![]() ,故
,故![]() 的取值范围是[
的取值范围是[![]() ,+∞).
,+∞).
试题解析:
(1)由题设得![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]()
![]() ,解得
,解得![]() .
.
因此椭圆![]() 的方程为
的方程为![]() .由抛物线
.由抛物线![]() 的方程为
的方程为![]() ,得
,得![]() .
.
设直线![]() 的方程为
的方程为![]() (
(![]() 存在),
存在),![]() ,
,![]() .
.
于是由![]() 消去
消去![]() 得
得![]() ,∴
,∴![]() ,①
,①
∴![]()
![]() ∴将①代入上式得
∴将①代入上式得![]() ,
,
故![]() .
.
(2)由(1)知,![]() ,∴
,∴![]() 和
和![]() 均为直角三角形,设直线
均为直角三角形,设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,且
,且![]() ,由
,由![]() 解得
解得![]() 或
或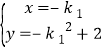 ,∴
,∴![]() ,同理可得
,同理可得![]() ,
,
∴![]() .
.
由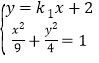 解得
解得![]() 或
或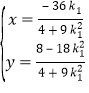 ,∴
,∴![]() ,
,
同理可得![]() ,
,
∴![]() ,
,
∴![]()
![]() 又∵
又∵![]() >0,∴
>0,∴![]() ≥
≥![]() .
.
故![]() 的取值范围是[
的取值范围是[![]() ,+∞).
,+∞).

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目