题目内容
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
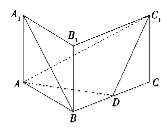
⑴求证:![]() ;
;
⑵求二面角![]() 的余弦值;
的余弦值;
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,根据直四棱柱的性质,得到
,根据直四棱柱的性质,得到![]() ,利用线面平行的判定定理,即可证得
,利用线面平行的判定定理,即可证得![]() ;(2)由
;(2)由![]() 是直棱柱,且
是直棱柱,且![]() ,故
,故![]() 、
、![]() 、
、![]() 两两垂直,建立空间直角坐标系
两两垂直,建立空间直角坐标系![]() ,求解平面
,求解平面![]() 和平面
和平面![]() 的法向量,求解两个向量所成的角,即可求解二面角的余弦值.
的法向量,求解两个向量所成的角,即可求解二面角的余弦值.
试题解析:⑴证明:连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
由![]() 是直三棱柱得四边形
是直三棱柱得四边形![]() 为矩形,
为矩形,![]()
![]() 的中点.
的中点.
又![]() 为
为![]() 中点,所以
中点,所以![]() 为
为![]() 中位线,所以
中位线,所以![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() .
.
⑵由![]() 是直棱柱,且
是直棱柱,且![]() ,故
,故![]() 、
、![]() 、
、![]() 两两垂直.
两两垂直.
如图建立空间直角坐标系![]() .
.
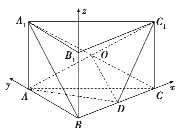
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则有
,则有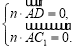 所以
所以![]()
取![]() ,得
,得![]() .
.
易知平面![]() 法向量为
法向量为![]() .
.
由二面角![]() 平面角是锐角,得
平面角是锐角,得![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
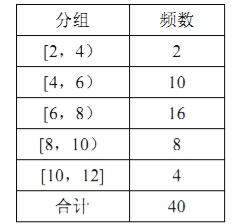
【题目】已知函数![]() 的定义域
的定义域![]() ,部分对应值如表,
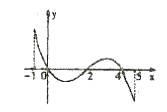
,部分对应值如表, ![]() 的导函数
的导函数![]() 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数![]() 的命题;
的命题;
|
|
|
|
|
|
|
|
|
|
|
|
①函数![]() 的值域为
的值域为![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③如果当![]() 时,
时, ![]() 最大值是
最大值是![]() ,那么
,那么![]() 的最大值为
的最大值为![]() ;
;
④当![]() 时,函数
时,函数![]() 最多有4个零点.
最多有4个零点.
其中正确命题的序号是_________.