题目内容
【题目】设△ABC的内角A、B、C所对的边分别为a、b、c，已知a＝1，b＝2，cos C＝
.
(Ⅰ)求△ABC的周长； (Ⅱ)求cos A的值．
【答案】(Ⅰ)5(Ⅱ) 
【解析】
试题分析：(Ⅰ)由余弦定理可求得c边，从而得到周长；(Ⅱ)由三边长度可利用余弦定理求得cos A的值
试题解析：(Ⅰ)∵c2＝a2＋b2－2abcos C＝1＋4－4×
＝4.-----------2分
∴c＝2.∴△ABC的周长为a＋b＋c＝1＋2＋2＝5.-----------4分
(Ⅱ) ∵cos C＝
，∴sin C＝
＝
＝
.---6分
∴sin A＝
＝
＝
.-------------------------------8分
∵a＜c，∴A＜C.故A为锐角，------------------------------9分
∴cos A＝
＝
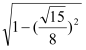＝.----------------10分
练习册系列答案
一线名师提优试卷系列答案
相关题目
