题目内容
(本小题满分14分)
在平面直角坐标系中,N为圆C: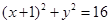 上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且
上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且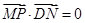 .
.
(Ⅰ)求动点P表示的曲线E的方程;
(Ⅱ)若曲线E与x轴的交点为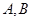 ,当动点P与A,B不重合时,设直线
,当动点P与A,B不重合时,设直线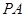 与
与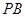 的斜率分别为
的斜率分别为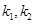 ,证明:
,证明: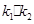 为定值;
为定值;
在平面直角坐标系中,N为圆C:
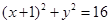 上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且
上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且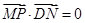 .
.(Ⅰ)求动点P表示的曲线E的方程;
(Ⅱ)若曲线E与x轴的交点为
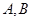 ,当动点P与A,B不重合时,设直线
,当动点P与A,B不重合时,设直线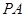 与
与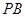 的斜率分别为
的斜率分别为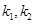 ,证明:
,证明: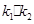 为定值;
为定值;(Ⅰ)解:由点M是DN的中点,又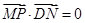 ,可知PM垂直平分DN.所以
,可知PM垂直平分DN.所以 ,又
,又 ,所以
,所以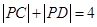 .
.
由椭圆定义知,点P的轨迹是以C,D为焦点的椭圆. ----------------------4分
设椭圆方程为 .
.
又 可得
可得
所以动点P表示的曲线E的方程为 . ----------------------8分
. ----------------------8分
(Ⅱ)证明:
易知A(-2,0),B(2,0). 设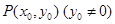 ,则
,则 ,即
,即 ,
,
则 ,
, , ----------------------10分
, ----------------------10分
即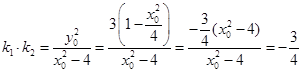 ,
,
∴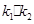 为定值
为定值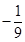 . -----------------------------------14分
. -----------------------------------14分
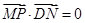 ,可知PM垂直平分DN.所以
,可知PM垂直平分DN.所以 ,又
,又 ,所以
,所以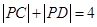 .
.由椭圆定义知,点P的轨迹是以C,D为焦点的椭圆. ----------------------4分
设椭圆方程为
 .
.又
 可得
可得
所以动点P表示的曲线E的方程为
 . ----------------------8分
. ----------------------8分(Ⅱ)证明:
易知A(-2,0),B(2,0). 设
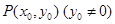 ,则
,则 ,即
,即 ,
, 则
 ,
, , ----------------------10分
, ----------------------10分即
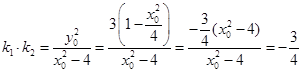 ,
, ∴
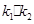 为定值
为定值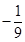 . -----------------------------------14分
. -----------------------------------14分略

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
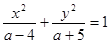 的焦点为定点,则焦点坐标是 .
的焦点为定点,则焦点坐标是 .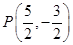 、
、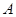 (-2,0)、
(-2,0)、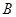 (2,0)。
(2,0)。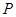 的椭
的椭 圆的标准方程;
圆的标准方程;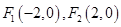 ,一曲线
,一曲线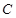 经过点
经过点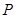 ,且
,且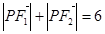
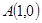 ,若
,若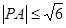 ,求点
,求点 的方程为:
的方程为: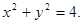 直线
直线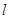 过点
过点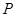 (1,2),且与圆
(1,2),且与圆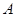 、
、 两点,若
两点,若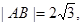 求直线
求直线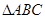 中,
中,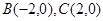 ,
,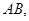
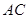 边上的中线长之和为30,则
边上的中线长之和为30,则
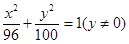
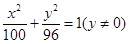
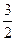 ),且点F(-1,0)为其左焦点.
),且点F(-1,0)为其左焦点.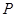 .为双曲线
.为双曲线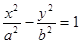 上的一点,
上的一点,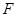 为一个焦点,以
为一个焦点,以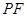 为直径的圆与圆
为直径的圆与圆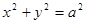 的位置关系是
的位置关系是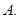 内切
内切 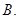 内切或外切
内切或外切 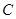 .外切
.外切 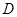 .相离或相交
.相离或相交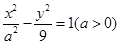 的渐近线方程为
的渐近线方程为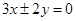 ,则
,则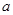 的值为( )
的值为( )