题目内容
若点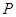 是以
是以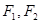 为焦点的椭圆
为焦点的椭圆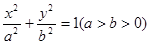 上一点,
上一点,
且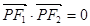 ,
,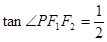 ,则此椭圆的离心率
,则此椭圆的离心率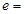
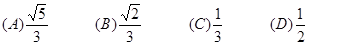
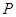 是以
是以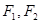 为焦点的椭圆
为焦点的椭圆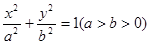 上一点,
上一点,且
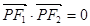 ,
,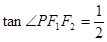 ,则此椭圆的离心率
,则此椭圆的离心率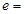
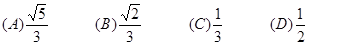
A
试题分析:如图,由
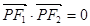 得:
得: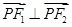 ,即有
,即有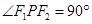 ,又因为
,又因为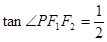 ,所以
,所以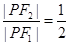 ,结合椭圆的特点得:
,结合椭圆的特点得: ,解得
,解得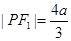 ,
, ,另外
,另外 ,在三角形
,在三角形 中,由勾股定理得:
中,由勾股定理得: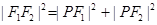 ,即有
,即有 ,解得
,解得 。故选A。
。故选A。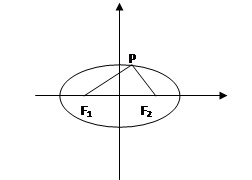
点评:解关于椭圆的问题,经常要用到椭圆的特点:椭圆上任一点到两焦点的距离之和等于
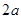 。
。
练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
题目内容
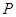 是以
是以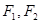 为焦点的椭圆
为焦点的椭圆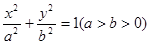 上一点,
上一点,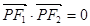 ,
,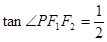 ,则此椭圆的离心率
,则此椭圆的离心率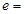
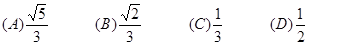
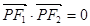 得:
得: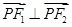 ,即有
,即有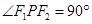 ,又因为
,又因为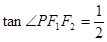 ,所以
,所以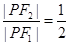 ,结合椭圆的特点得:
,结合椭圆的特点得: ,解得
,解得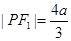 ,
, ,另外
,另外 ,在三角形
,在三角形 中,由勾股定理得:
中,由勾股定理得: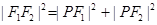 ,即有
,即有 ,解得
,解得 。故选A。
。故选A。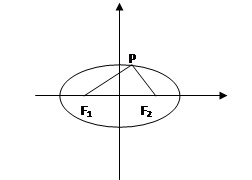
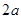 。
。
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案