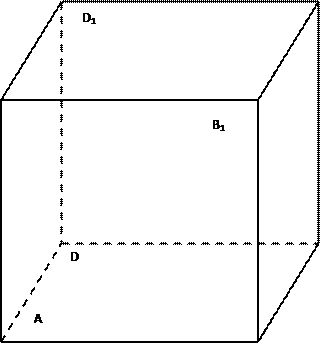题目内容
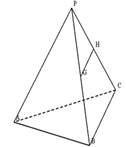
(1)证明直线和平面垂直的判定定理,即已知:如图1, 且
且 ,
, 求证:
求证:
(2)请用直线和平面垂直的判定定理证明:如果一条直线垂直于两个平行平面中的一个,那么它也垂直于另一个平面,即
已知:如图2,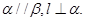 求证:
求证:


 且
且 ,
, 求证:
求证:
(2)请用直线和平面垂直的判定定理证明:如果一条直线垂直于两个平行平面中的一个,那么它也垂直于另一个平面,即
已知:如图2,
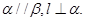 求证:
求证:


(Ⅰ)证明:设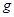 是平面
是平面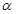 内的任一直线,直线
内的任一直线,直线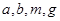 所在的方向向量分别为
所在的方向向量分别为 ,
,
∵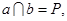
∴向量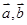 不共线,由平面向量的基本定理知,对于平面
不共线,由平面向量的基本定理知,对于平面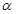 内向量
内向量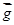 ,存在唯一的有序实数对
,存在唯一的有序实数对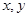 ,满足:
,满足: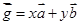
∵ ,即有
,即有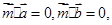
∴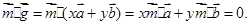
∴ 即
即
由直线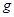 的任意性知,
的任意性知, 命题得证。 …………………………………6分
命题得证。 …………………………………6分
(Ⅱ)设经过直线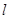 的平面
的平面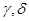 分别与
分别与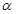 交于
交于 ,与
,与 交于
交于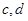 ,则
,则
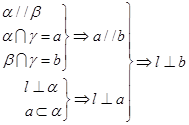
同理可证
注意到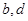 是相交直线,因此
是相交直线,因此

 是平面
是平面 内的任一直线,直线
内的任一直线,直线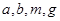 所在的方向向量分别为
所在的方向向量分别为 ,
,∵
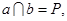
∴向量
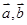 不共线,由平面向量的基本定理知,对于平面
不共线,由平面向量的基本定理知,对于平面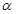 内向量
内向量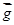 ,存在唯一的有序实数对
,存在唯一的有序实数对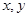 ,满足:
,满足: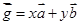
∵
 ,即有
,即有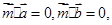
∴
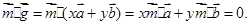
∴
 即
即
由直线
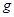 的任意性知,
的任意性知, 命题得证。 …………………………………6分
命题得证。 …………………………………6分(Ⅱ)设经过直线
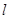 的平面
的平面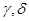 分别与
分别与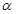 交于
交于 ,与
,与 交于
交于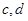 ,则
,则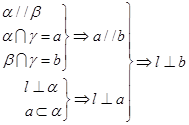
同理可证

注意到
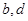 是相交直线,因此
是相交直线,因此

略

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
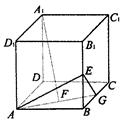
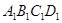 中,E、F、G分别是
中,E、F、G分别是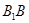 、AB、BC的中点.
、AB、BC的中点.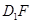 ⊥平面AEG;
⊥平面AEG;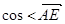 ,
,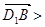
 —
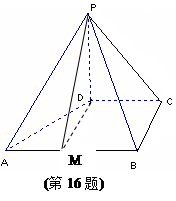
—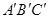 中,点D是BC的中点,欲过点
中,点D是BC的中点,欲过点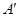 作一截面与平面
作一截面与平面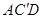 平行,问应当怎样画线,并说明理由。
平行,问应当怎样画线,并说明理由。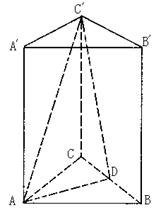
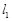 与
与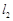 互相平行的一个充分条件是
互相平行的一个充分条件是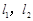 都平行于同一平面
都平行于同一平面