题目内容
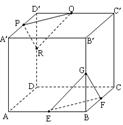
在正方体AC¢中,E、F、G、P、Q、R分别是所在棱AB、BC、BB¢、A¢D¢、D¢C¢、DD¢的中点,求证:平面PQR∥平面EFG。
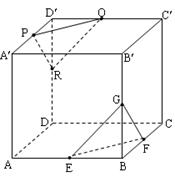

证明:连结A`C`、AC,
∵P、Q分别是A`D`、C`D`的中点
∴PQ//A`C`,
同理EF//AC,
同理GF//PR,
又PR∩PQ=P,GF∩EF=F
∴平面PQR//平面EFG

∵P、Q分别是A`D`、C`D`的中点
∴PQ//A`C`,
同理EF//AC,
同理GF//PR,
又PR∩PQ=P,GF∩EF=F
∴平面PQR//平面EFG
略

练习册系列答案
相关题目
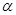 ,
,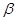 是空间两个平面,则下列命题中,逆命题不成立的是( )
是空间两个平面,则下列命题中,逆命题不成立的是( )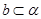 时,若b⊥
时,若b⊥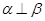
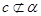 时,若c∥
时,若c∥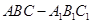 中,
中, ,
, ,点
,点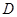 在
在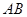 上.
上.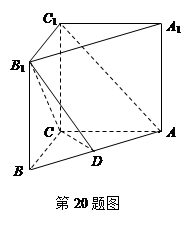
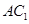 ∥平面
∥平面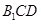 ;
;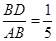 时,求二面角
时,求二面角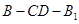 的余弦值.
的余弦值.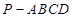 中,
中, 面
面 ,四边形
,四边形 是
是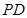 的中点,
的中点,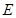 是
是 的中点
的中点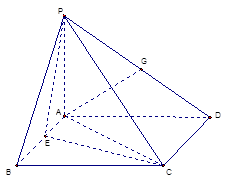
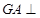 面
面 ;
; 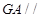 面
面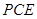 .
.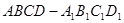 中,
中,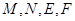 分别是棱
分别是棱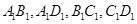 的中点.
的中点. 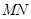 ∥平面
∥平面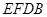 ;
;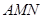 ∥平面
∥平面
 是异面直线,直线
是异面直线,直线 ,则
,则 与
与 的位置关系是
的位置关系是 且
且 ,
, 求证:
求证:
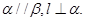 求证:
求证:


 是
是 的直径,
的直径, 是圆周上不同于
是圆周上不同于 、
、 的任意一点,
的任意一点, 平面
平面 ,则四面体
,则四面体 的四个面中,直角三角形的个数有( )
的四个面中,直角三角形的个数有( )
 个
个 个
个 个
个 个
个 中,
中,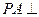 底面ABC,
底面ABC,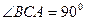 ,AP="AC," 点
,AP="AC," 点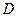 ,
, 分别在棱
分别在棱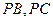 上,且BC//平面ADE
上,且BC//平面ADE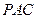 ;
; (Ⅱ)当二面角
(Ⅱ)当二面角 为直二面角时,求多面体ABCED与PAED的体积比。
为直二面角时,求多面体ABCED与PAED的体积比。