题目内容
15.把座位编号为1,2,3,4,5,6的6张电影票分给甲、乙、丙、丁四个人,每人至少分一张,至多分两张,且分得的两张票必须是连号,那么不同分法种数为( )| A. | 240 | B. | 144 | C. | 196 | D. | 288 |
分析 根据题意,先将票分为符合题意要求的4份;可以转化为将1、2、3、4、5、6这六个数用3个板子隔开,分为四部分且不存在三连号的问题,用插空法易得其情况数目,再将分好的4份对应到4个人,由排列知识可得其情况数目,由分步计数原理,计算可得答案.
解答 解:根据题意,分2步进行分析:
①、先将票分为符合条件的4份;
由题意,4人分6张票,且每人至少一张,至多两张,则两人一张,2人2张,且分得的票必须是连号,
相当于将1、2、3、4、5、6这六个数用3个板子隔开,分为四部分且不存在三连号;
易得在5个空位插3个板子,共有C53=10种情况,但其中有四种是1人3张票的,故有10-4=6种情况符合题意,
②、将分好的4份对应到4个人,进行全排列即可,有A44=24种情况;
则共有6×24=144种情况;
故选:B.
点评 本题考查排列、组合的应用,解答的关键是将分票的问题转化为将6个数如何分为四部分的问题,用插空法解决问题.

练习册系列答案
相关题目
3.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为60°,则$\vec b•(\vec b-\vec a)$等于( )
| A. | 1 | B. | 3 | C. | 2-$\sqrt{3}$ | D. | 4-$\sqrt{3}$ |
20.下列各组函数f(x)与g(x)的图象相同的是( )
| A. | f(x)=(x-1)0与g(x)=1 | B. | f(x)=x与g(x)=$\sqrt{x^2}$ | ||
| C. | f(x)=$\frac{{{x^2}-4}}{x-2}$,g(x)=x+2 | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}x(x≥0)\\-x(x<0)\end{array}$ |
16.已知$sinx=\frac{{\sqrt{3}}}{3}$,$x∈({\frac{π}{2},\;π})$,则x等于( )
| A. | $\frac{π}{2}+arcsin\frac{{\sqrt{3}}}{3}$ | B. | $α≠\frac{kπ}{2}(k∈Z)$ | C. | $arcsin\frac{{\sqrt{3}}}{3}$ | D. | $π-arcsin\frac{{\sqrt{3}}}{3}$ |
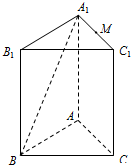 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC.